Question

A、B两名同学在一个学校上学，B同学上学的路上经过A同学家．A同学步行，B同学骑自行车，某天，A，B两名同学同时从家出发到学校，如图，l_A表示A同学离B同学家的路程s_A（m）与行走时间t（min）之间的函数关系图象，l_B表示B同学离家的路程sB（m）与行走时间t（min）之间的函数关系图象．

（1）A，B两名同学的家相距__________m．

（2）B同学走了一段路后，自行车发生故障，进行修理，修理自行车所用的时间是__________min．

（3）B同学出发后__________min与A同学相遇．

（4）求出A同学离B同学家的路程s_A与时间t的函数关系势．

Answer 1

【考点】一次函数的应用．

【分析】（1）从图上可看出A，B两名同学的家相距2100米．

（2）修理的时间就是路程不变的时间是15﹣5=10min．

（3）从图象看出30min时，两个图象相交，所以30min时相遇．

（4）S_A和t的函数关系是一次函数，设函数是为S=kx+t，过（0，2100）和（33，4500），从而可求出关系式．

【解答】解：根据图象知：（1）A，B两名同学的家相距2100米；

故答案为：2100；

（2）修理自行车的时间为：15﹣5=10min；

故答案为：10；

（3）B同学出发后30min时A同学相遇．；

故答案为：30；

（4）设函数是为S_A=kx+t，且过（0，2100）和（30，4500），

∴，

解得：，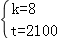

∴A同学离B同学家的路程s_A与时间t的函数关系式：y=8x+2100．

【点评】本题考查一次函数的应用，关键从图象上获取信息，根据图象的确定函数形式，设出函数式，代入已知点确定函数式，求变量或函数值或交点．