
【题目】如图,在等腰梯形ABCD中,AD∥BC,M、N分别为AD、BC的中点,E、F分别是BM、CM的中点.
⑴求证:△ABM≌△DCM;
⑵四边形MENF是什么图形?请证明你的结论;
⑶若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?并请说明理由.

【答案】(1)见解析;(2)四边形MENF是菱形,理由见解析;(3)梯形的高等于底边BC的一半,理由见解析
【解析】
(1)已知四边形ABCD为等腰梯形,M为AD的中点,推出AB=DC,∠A=∠D,AM=DM故可证明三角形全等;
(2)由(1)证明三角形全等得出MB=MC,根据三角形中位线定理,推出四边形MENF是菱形;
(3)由四边形MENF是正方形,得出∠BMC= 90°,△BMC是等腰直角三角形,根据等腰三角形三线合一的定理和直角三角形斜边上的中线可推出MN⊥BC且MN=![]() BC.
BC.
证明:(1)∵四边形ABCD是等腰梯形,
∴∠A= ∠D, AB=DC.
∵AM=DM,
∴△ABM≌△DCM.;
(2)四边形MENF是菱形,理由如下:
∵ △ABM≌△DCM,
∴MB=MC.
∵M、N 、 E、F分别为AD、BC 、 BM、CM的中点,
∴NE=![]() MC=MF, NF=
MC=MF, NF=![]() MB=ME,
MB=ME,
则NE=MF=NF=ME , 即四边形MENF是菱形;
(3)梯形的高等于底边BC的一半. 连接MN,
∵四边形MENF是正方形,
∴∠BMC= 90°.
∵BM=CM, ∴△BMC是等腰直角三角形
又∵N点是BC的中点
∴MN⊥BC且MN=![]() BC
BC


科目:初中数学 来源: 题型:
【题目】班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1).
(1)请根据图1,回答下列问题:
①这个班共有名学生,发言次数是5次的男生有人、女生有人;
②男、女生发言次数的中位数分别是次和次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数和全班增加的发言总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
A.20( ![]() +1)
+1)
B.20( ![]() ﹣1)
﹣1)
C.200
D.300
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题.
例题:若m2+2mn+2n26n+9=0,求m和n的值.
解:∵m2+2mn+2n26n+9=0即:
∴m2+2mn+n2+n26n+9=0
∴![]()
∴即:m+n=0,n-3=0
∴m=3,n=3
(1)若![]() ,求
,求![]() 的值.
的值.
(2)若三角形三边a,b,C都是正整数,且满足![]() ,判断三角形的形状.
,判断三角形的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用同样大小的黑、白两种颜色的棋子摆成正方形图案,则下列说法中:①第n个正方形包含(4n+4)枚白色棋子;②第n个正方形包含n2枚黑色棋子;③第n个正方形包含(n+2)2﹣n2枚白色棋子;④第n个正方形一共包含(n+1)2枚棋子,正确的个数是( )
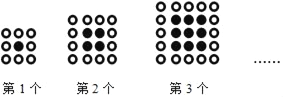
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com