
【题目】如图,矩形![]() 中,
中,![]() cm,
cm,![]() cm,动点
cm,动点![]() 以2cm╱s的速度从点
以2cm╱s的速度从点![]() 开始沿折线
开始沿折线![]() —
—![]() 向终点
向终点![]() 运动,动点
运动,动点![]() 以2cm╱s的速度从点D开始沿折线
以2cm╱s的速度从点D开始沿折线![]() —
—![]() 向点终点
向点终点![]() 运动.如果点
运动.如果点![]() ,
,![]() 同时出发,设点
同时出发,设点![]() 运动的时间为t秒.
运动的时间为t秒.
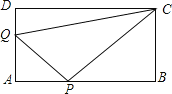
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求△CPQ的面积(可用含有t的代数式表示).
【答案】(1)![]() ;(2)①0≤x≤3,s=36-12t+2t2;3<x≤6,s=18;6<x≤9,s=2t2-36t+162
;(2)①0≤x≤3,s=36-12t+2t2;3<x≤6,s=18;6<x≤9,s=2t2-36t+162
【解析】
(1)用含t的式子表示AQ,AP,根据等腰直角三角形的性质即可求解;
(2)根据题意分①Q在线段AD上,P在线段AB上,②Q,P都在线段AB上,③Q在线段AB上,P在线段BC上依次求解即可.
(1)∵矩形![]() 中,
中,![]() cm,
cm,![]() cm,
cm,
∴AD=6cm,CD=12cm,
依题意得AQ=6-2t,AP=2t,
∵△QAP为等腰直角三角形
∴AQ= AP,即6-2t=2t,
解得![]()
故![]() 时,△QAP为等腰直角三角形
时,△QAP为等腰直角三角形
(2)当①Q在线段AD上,P在线段AB上,
即0≤t≤3时,DQ=2t,AQ=6-2t,AP=2t,BP=12-2t,
∴S△CPQ=S四边形ABCD-S△CDQ-S△APQ-S△BCP
=AB×BC-![]() ×CD×DQ-
×CD×DQ-![]() ×AP×AQ-
×AP×AQ-![]() ×BP×BC
×BP×BC
= 12×6-![]() ×12×2t-
×12×2t-![]() ×2t×(6-2t)-
×2t×(6-2t)-![]() ×(12-2t)×6
×(12-2t)×6
=36-12t+2t2
②Q,P都在线段AB上,即3<t≤6时,
AQ=2t-6,AP=2t,
∴PQ= AP-AQ=6,
S△CPQ=![]() ×QP×BC=
×QP×BC=![]() ×6×6=18;
×6×6=18;
③Q在线段AB上,P在线段BC上,即6<t≤9时,
AQ=2t-6,BQ=AB-AQ=18-2t,BP=2t-12,CP=BC-BP=18-2t,
∴S△CPQ=![]() ×CP×BQ=
×CP×BQ=![]() ×(18-2t)×(18-2t)= 2t2-36t+162
×(18-2t)×(18-2t)= 2t2-36t+162
故0≤t≤3,s=36-12t+2t2;
3<t≤6,s=18;
6<t≤9,s=2t2-36t+162.


科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是矩形,已知PB=PC.
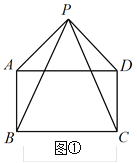
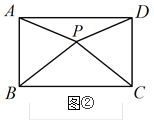
(1)若P是矩形外一点,求证:PA=PD;
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
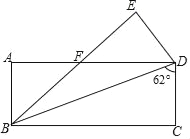
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
科目:初中数学 来源: 题型:
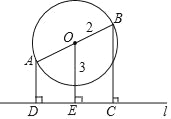
【题目】如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB不垂直于直线l,过点A,B分别作直线l的垂线,垂足分别为点D,C,则四边形ABCD的面积的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个有理数都能写成分数的形式(整数可以看作是分母为1的分数).我们知道:0.12可以写![]() ,0.123可以写成
,0.123可以写成![]() ,因此,有限小数是有理数那么无限循环小数是有理数吗?下面以循环小数2.61545454…=
,因此,有限小数是有理数那么无限循环小数是有理数吗?下面以循环小数2.61545454…=![]() 为例,进行探索:
为例,进行探索:
设x=![]() ,①
,①
两边同乘以100得:100x=![]() ,②
,②
②-①得:99x=261.54-![]() =258.93,
=258.93,
∴x=![]()
因此, ![]() 是有理数.
是有理数.
(1)直接用分数表示循环小数![]() =______.
=______.
(2)试说明![]() 是一个有理数,即能用一个分数表示.
是一个有理数,即能用一个分数表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向左移动2cm到达A点,再向左移动3cm到达B点,然后向右移动9cm到达C点。
![]()
(1)用1个单位长度表示1cm,请你在数轴上表示出A. B. C三点的位置;
(2)把点C到点A的距离记为CA,则CA=______cm.
(3)若点B以每秒2cm的速度向左移动,同时A. C点分别以每秒1cm、4cm的速度向右移动。设移动时间为t秒,试探索:CAAB的值是否会随着t的变化而改变?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com