
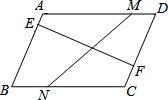
 如图,四边形ABCD为平行四边形,M,N两点分别从点D到点A、点B到点C运动,速度相同;E,F两点分别从点A到点B,点C到点D运动,速度相同.它们之间用橡皮筋连接.
如图,四边形ABCD为平行四边形,M,N两点分别从点D到点A、点B到点C运动,速度相同;E,F两点分别从点A到点B,点C到点D运动,速度相同.它们之间用橡皮筋连接.分析 (1)由四边形ABCD为平行四边形,根据平行四边形的对角线互相平分,即可判定;
(2)首先顺次连接EN、NF、FM、ME,证得四边形ENFM为平行四边形,则EF与MN相互平分.
解答 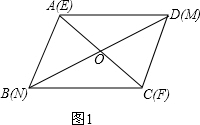 (1)解:没有出发时,这两条绳子相互平分.理由如下:
(1)解:没有出发时,这两条绳子相互平分.理由如下:
如图1,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
即EF与MN相互平分;
(2)解:若同时出发,这两条绳子还有(1)中的结论.理由如下:
∵四边形ABCD是平行四边形,
∴∠A=∠C.
又∵M、N分别从D到A、从B到C,速度相同,E、F分别从A到B、从C到D,速度相同,
∴AE=CF,AM=CN,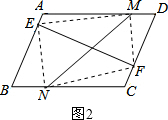
∴在△AEM与△CFN中,
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠C}\\{AM=CN}\end{array}\right.$,
∴△AEM≌△CFN(SAS),
∴EM=FN.
同理可得:EN=MF,
∴四边形ENFM为平行四边形,
∴EF与MN相互平分.
点评 本题考查了平行四边形的判定与性质以及全等三角形的判定与性质.解答(2)题的关键是证得四边形ENFM为平行四边形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
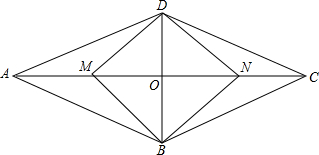 如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.
如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
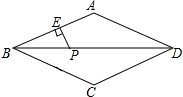 如图,P是菱形ABCD对角线BD上一点,PE⊥AB于E,PE=4cm,则点P到BC的距离是( )
如图,P是菱形ABCD对角线BD上一点,PE⊥AB于E,PE=4cm,则点P到BC的距离是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 8cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com