
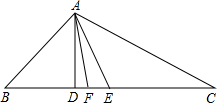
 如图,完成下面几何语言的表达.
如图,完成下面几何语言的表达.分析 ①根据三角形的定义和垂直的定义解答;②根据三角形的中线的定义和线段的中点的定义解答;③根据三角形的角平分线和角平分线的定义解答.
解答 解:①∵AD是△ABC的高(已知);
∴AD⊥BC,∠ADB=∠ADC=90°.
②∵AE是△ABC的中线(已知),
∴BE=CE=$\frac{1}{2}$BC,BC=2BE=2CE;
③∵AF是△ABC的角平分线(已知),
∴∠BAF=∠CAF=$\frac{1}{2}$∠BAC,
∠BA=2∠BAF=2∠CAF.
故答案为:ADB,∠ADC,90,BE,CE,BC,BC,BE,CE,BAF,CAF,BAC,BCA,BAF,CAF.
点评 本题考查了三角形的角平分线,中线,高,熟记各定义是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com