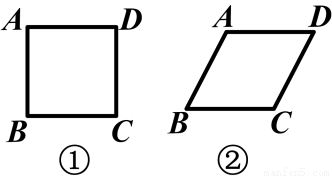
(2014广东广州)将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变．当∠B＝90°时，如图①，测得AC＝2．当∠B＝60°时，如图②，AC＝( )
A．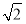
B．2
C．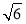
D．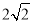
教材全解字词句篇系列答案科目：初中数学 来源：2015年人教版初中数学八年级19.1.2练习卷（解析版）2 题型：解答题
某商店零售一种商品，其质量x(kg)与售价y(元)之间的关系如下表：
x／kg | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y／元 | 2.4 | 4.8 | 7.2 | 9.6 | 12 | 14.4 | 16.8 | 19.2 |
根据销售经验可知，在此处零买这种商品的顾客所买商品均未超过8kg．
(1)由上表推出售价y(元)关于质量x(kg)的函数解析式，并画出函数的图象；
(2)李大婶购买这种商品5.5kg，应付多少元钱？
查看答案和解析>>
科目：初中数学 来源：2015年人教版初中数学八年级18专题突破卷（解析版） 题型：解答题
如图，E，F分别是□ABCD的AD，BC边上的点，且AE＝CF．
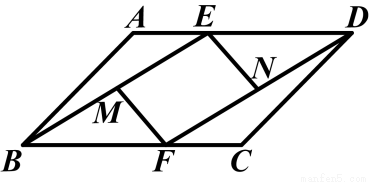
(1)求证：△ABE≌△CDF；
(2)若M，N分别是BE，DF的中点，连接MF，EN，试判断四边形MFNE是怎样的四边形，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源：2015年人教版初中数学八年级18.2.3练习卷（解析版）2 题型：解答题
操作示例
对于边长为a的两个正方形ABCD和EFGH，按图1所示的方式摆放，沿虚线BD、EG剪开后，可以按图1所示的移动方式拼接为四边形BNED．从拼接的过程容易得到结论：
①四边形BNED是正方形；
②S正方形ABCD＋S正方形EFGH＝S正方形BNED．
实践与探究
(1)对于边长分别为a，b(a＞b)的两个正方形ABCD和EFGH，按图2所示的方式摆放，连接DE，过点D作DM⊥DE，交AB于点M，过点M作MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N．
①证明：四边形MNED是正方形，并用含a，b的代数式表示正方形MNED的面积；
②在图2中，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED，请简略说明你的拼接方法(类比图1，用数字表示对应的图形)；
(2)对于n(n是大于2的自然数)个任意的正方形，能否通过若干次拼接，将其拼接成为一个正方形？请简要说明你的理由．
查看答案和解析>>
科目：初中数学 来源：2015年人教版初中数学八年级18.2.3练习卷（解析版）2 题型：解答题
如图，已知在Rt△ABC中，∠ABC＝90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线AB平移至△FEG，DE、FG相交于点H．
(1)判断线段DE、FG的位置关系，并说明理由：
(2)连接CG，求证：四边形CBEG是正方形．(提示：旋转前后，图形中对应的角和对应的边分别相等)
查看答案和解析>>
科目：初中数学 来源：2015年人教版初中数学八年级18.2.3练习卷（解析版） 题型：简答题
（2013铁岭）如图，△ABC中，AB＝AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE＝OD，连接AE，BE．
（1）求证：四边形AEBD是矩形．
（2）当△ABC满足什么条件时，矩形AEBD是正方形？并说明理由．
查看答案和解析>>
科目：初中数学 来源：2015年人教版初中数学八年级18.2.2练习卷（解析版） 题型：解答题
如图，□ABCD的对角线AC的垂直平分线与AD、BC、AC分别交于点E、F、O，求证：四边形AFCE是菱形．
查看答案和解析>>
科目：初中数学 来源：2015年人教版初中数学八年级18.1.2练习卷（解析版） 题型：解答题
(2012江苏泰州)如图，四边形ABCD中，AD∥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE＝CF．求证：四边形ABCD是平行四边形．
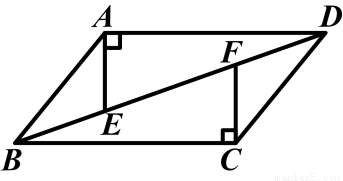
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的自变量x的取值范围在数轴上可表示为( )
