
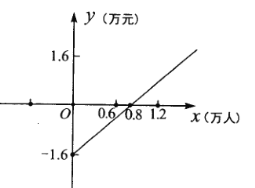
【题目】某公共汽车线路每天运营毛利润![]() (万元)与乘客量
(万元)与乘客量![]() (万人)成一次函数关系,其图象如图所示.目前通过监测发现每天平均乘客量为0.6万人次,由于运营成本较高,这条线路处于亏损状态.(毛利润=票价总收入一运营成本)
(万人)成一次函数关系,其图象如图所示.目前通过监测发现每天平均乘客量为0.6万人次,由于运营成本较高,这条线路处于亏损状态.(毛利润=票价总收入一运营成本)
(1)求该线路公共汽车的单程票价和每天运营成本分别为多少元.
(2)公交公司为了扭亏,若要使每天运营毛利润在0.2~0.4万元之间(包括0.2和0.4),求平均每天的乘客量![]() 的范围.
的范围.
(3)据实际情况,发现该线路乘客量稳定,公交公司决定适当提高票价,当单程票价每提高1元时,每天平均乘客量相应减少0.05万人次,设这条线路的单程票价提高![]() 元(
元(![]() ).当
).当![]() 为何值时,该线路每天运营总利润最大,并求出最大的总利润.
为何值时,该线路每天运营总利润最大,并求出最大的总利润.
【答案】(1)2元/人,1.6万元;(2)![]() ;(3)当
;(3)当![]() 时,该公共汽车线路每天运营总利润最大,最大的总利润为0.4万元.
时,该公共汽车线路每天运营总利润最大,最大的总利润为0.4万元.
【解析】
(1)根据图象分析即可;
(2)利用待定系数法求出一次函数解析式,代入求值即可得到x的范围;
(3)设总利润为![]() ,根据题意
,根据题意![]() ,利用二次函数求最值即可.
,利用二次函数求最值即可.
解:(1)图象与y轴的交点纵坐标为每天的运营成本,当0.8万人次时毛利润为0,故
单程票价:![]() (元/人),每天的运营成本为1.6万元.
(元/人),每天的运营成本为1.6万元.
(2)设![]() ,将
,将![]() ,
,![]() 代入得:
代入得:![]() ,
,![]() .
.
∴![]() .
.
因为![]() ,故
,故![]() 随
随![]() 的增大而增大,
的增大而增大,
当![]() ,
,![]() .
.
当![]() 时,
时,![]() .
.
所以![]() .
.
(3)设总利润为![]() ,则
,则![]() ,
,
整理得:![]() ,
,
当![]() 时,不在
时,不在![]() 内,当
内,当![]() 时,
时,![]() 有最大值为0.4万元.
有最大值为0.4万元.
答:当![]() 时,该公共汽车线路每天运营总利润最大,最大的总利润为0.4万元.
时,该公共汽车线路每天运营总利润最大,最大的总利润为0.4万元.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
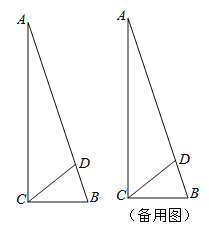
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边上一点,且
是斜边上一点,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的
的![]() 与边
与边![]() 相切,切点为
相切,切点为![]() 的中点
的中点![]() ,
,![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
(i)求![]() 的半径;
的半径;
(ⅱ)连接![]() ,试探究
,试探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
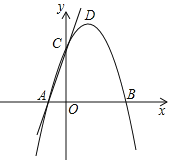
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点C,点D时抛物线的顶点
轴交于点C,点D时抛物线的顶点
(1)求抛物线的解析式和直线![]() 的解析式;
的解析式;
(2)试探究:在抛物线上是否存在点P,使得以点![]() 为顶点,
为顶点,![]() 为直角边的三角形是直角三角形,若存在,请求出,请求出符合条件的点P的坐标;若不存在,请说明理由.
为直角边的三角形是直角三角形,若存在,请求出,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
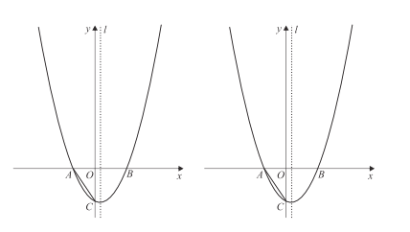
【题目】如图,已知抛物![]() 经过点
经过点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() ,其中
,其中![]() 点坐标为
点坐标为![]() ,对称轴
,对称轴![]() 为直线
为直线![]() .
.
(1)求抛物线的解析式;
(2) 在![]() 轴上方有一点
轴上方有一点![]() , 连接
, 连接![]() 后满足
后满足![]() , 记
, 记![]() 的面积为
的面积为![]() , 求当
, 求当![]() 时点
时点![]() 的坐标
的坐标
(3)在![]() 的条件下,当点
的条件下,当点![]() 恰好落在抛物线上时,将直线
恰好落在抛物线上时,将直线![]() 上下平移,平移后的
上下平移,平移后的![]() 时点
时点![]() 的坐标;直线
的坐标;直线![]() 与抛物线交于
与抛物线交于![]() 两点(
两点(![]() 在
在![]() 的左侧),若以点
的左侧),若以点![]() 为顶点的三角形是直角三角形,求出
为顶点的三角形是直角三角形,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() .以
.以![]() 为一边作等边三角形
为一边作等边三角形![]() ,点
,点![]() 在第二象限.
在第二象限.
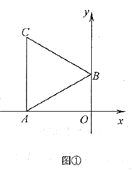
(Ⅰ)如图①,求点![]() 的坐标;
的坐标;
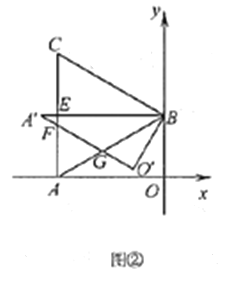
(Ⅱ)将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,点
,点![]() 旋转后的对应点为
旋转后的对应点为![]() .
.
①如图②,当旋转角为30°时,![]() 与
与![]() 分别交于点
分别交于点![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 与
与![]() 公共部分面积
公共部分面积![]() 的值;
的值;
②若![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 长的取值范围(直接写出结果即可).
长的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为![]() ,中轴轴心
,中轴轴心![]() 到地面的距离
到地面的距离![]() 为
为![]() ,后轮中心
,后轮中心![]() 与中轴轴心
与中轴轴心![]() 连线与车架中立管
连线与车架中立管![]() 所成夹角
所成夹角![]() ,后轮切地面
,后轮切地面![]() 于点
于点![]() .为了使得车座
.为了使得车座![]() 到地面的距离
到地面的距离![]() 为
为![]() ,应当将车架中立管
,应当将车架中立管![]() 的长设置为_____________
的长设置为_____________![]() .
.
(参考数据: ![]()
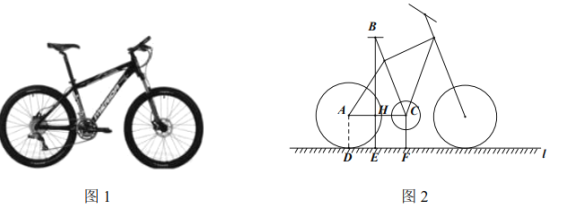
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边
ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边![]() CDE.
CDE.
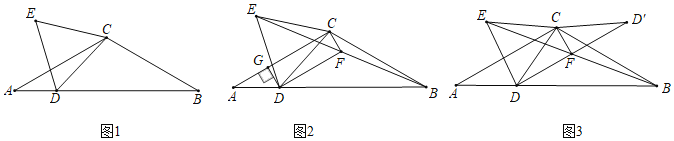
(1)如图1,若∠CDB=45°,AB=6,求等边![]() CDE的边长;
CDE的边长;
(2)如图2,点D在AB边上移动过程中,连接BE,取BE的中点F,连接CF,DF,过点D作DG⊥AC于点G.
①求证:CF⊥DF;
②如图3,将![]() CFD沿CF翻折得
CFD沿CF翻折得![]() CF
CF![]() ,连接B
,连接B![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
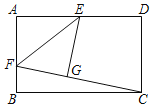
【题目】如图,矩形ABCD中,AB=8,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意外创伤随时可能发生,急救是否及时、妥善,直接关系到病人的安危.为普及急救科普知识,提高学生的急救意识与现场急救能力,某校开展了急救知识进校园培训活动.为了解七、八年级学生(七、八年级各有600名学生)的培训效果,该校举行了相关的急救知识竞赛.现从两个年级各随机抽取20名学生的急救知识竞赛成绩(百.分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,78,81,72,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 | |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 | c |
八年级 | 78 | d | 80.5 |
应用数据:
(1)由上表填空:a= ;b= ;c= ;d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在80分及以上的共有多少人?
(3)你认为哪个年级的学生对急救知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com