
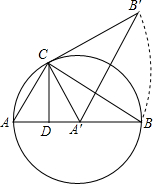
 如图,点C是以AB为直径的圆周上一点,CD⊥AB于点D,已知AD=1,DB=3,现将三角形ABC绕顶点C逆时针旋转,当顶点A的对应点A′落在边AB的起始位置上即停止转动,则点B转过的路径长为$\frac{2\sqrt{3}}{3}$π.
如图,点C是以AB为直径的圆周上一点,CD⊥AB于点D,已知AD=1,DB=3,现将三角形ABC绕顶点C逆时针旋转,当顶点A的对应点A′落在边AB的起始位置上即停止转动,则点B转过的路径长为$\frac{2\sqrt{3}}{3}$π. 分析 根据圆周角定理得到∠ACB=90°,再证明Rt△ACD∽Rt△ABC,利用相似比可计算出AC=2,接着根据勾股定理计算出BC=2$\sqrt{3}$,余弦定义可得到∠A=60°,然后根据旋转的性质得CA=CA′,∠ACA′=∠BCB′,则可判断△CAA′为等边三角形,所以∠ACA′=60°=∠BCB′=60°,最后利用弧长公式计算$\widehat{BB′}$的长度即可.
解答 解:∵AB为直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠ADC=90°,
∵∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,即$\frac{AC}{1+3}$=$\frac{1}{AC}$,
∴AC=2,
在Rt△ACB中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
在Rt△ACD中,∵cosA=$\frac{AD}{AC}$=$\frac{1}{2}$,
∴∠A=60°,
∵顶点A的对应点A′落在边AB的起始位置上,
∴CA=CA′,∠ACA′=∠BCB′,
∴△CAA′为等边三角形,
∴∠ACA′=60°,
∴∠BCB′=60°,
∴$\widehat{BB′}$的长度=$\frac{60•π•2\sqrt{3}}{180}$=$\frac{2\sqrt{3}}{3}$π,
即点B转过的路径长为$\frac{2\sqrt{3}}{3}$π.
故答案为$\frac{2\sqrt{3}}{3}$π.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是求出旋转角.


科目:初中数学 来源: 题型:选择题
| A. | 3967.29×103元 | B. | 3.96729×1011元 | C. | 0.396729×1011元 | D. | 3.96729×108元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
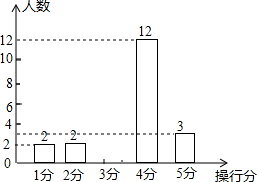 某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:
某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:| 操行分得分 | 1分 | 2分 | 3分 | 4分 | 5分 |
| 人数 | 2 | 4 | 9 | 30 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 47和49 | B. | 48和49 | C. | 47和46 | D. | 48和46 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知常数a(a是整数)满足下面两个要求:
已知常数a(a是整数)满足下面两个要求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知图1、图2、图3都是4×5的方格纸,其中每个小正方形的边长均为1cm,每个小正方形的顶点称为格点.
已知图1、图2、图3都是4×5的方格纸,其中每个小正方形的边长均为1cm,每个小正方形的顶点称为格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com