
【题目】如图,点E是正方形ABCD的边CD上一点,以A为圆心,AB为半径的弧与BE交于点F,则∠EFD=_____°.
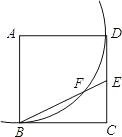
【答案】45
【解析】
由四边形ABCD为正方形及半径相等得到AB=AF=AD,∠ABD=∠ADB=45°,利用等边对等角得到两对角相等,由四边形ABFD的内角和为360度,得到四个角之和为270,利用等量代换得到∠ABF+∠ADF=135°,进而确定出∠1+∠2=45°,由∠EFD为三角形DEF的外角,利用外角性质即可求出∠EFD的度数.
∵正方形ABCD,AF,AB,AD为圆A半径,
∴AB=AF=AD,∠ABD=∠ADB=45°,
∴∠ABF=∠AFB,∠AFD=∠ADF,
∵四边形ABFD内角和为360°,∠BAD=90°,
∴∠ABF+∠AFB+∠AFD+∠ADF=270°,
∴∠ABF+∠ADF=135°,
∵∠ABD=∠ADB=45°,即∠ABD+∠ADB=90°,
∴∠1+∠2=135°90°=45°,
∵∠EFD为△DEF的外角,
∴∠EFD=∠1+∠2=45°.
故答案为:45


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
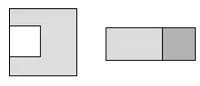
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2
D.a2-ab=a(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用如图的两个分格均匀的转盘![]() 、
、![]() 做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
![]() 用列表格或画树状图的方法表示游戏所有可能出现的结果.
用列表格或画树状图的方法表示游戏所有可能出现的结果.
![]() 求甲、乙两人获胜的概率.
求甲、乙两人获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:如图,
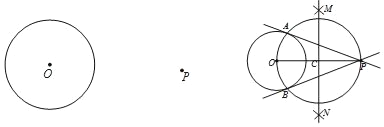
(1)连接OP,作线段OP的垂直平分线MN交OP于点C.
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点.
(3)作直线PA,PB.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是 ;由此可证明直线PA,PB都是⊙O的切线,其依据是 .请写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程kx2﹣(4k+1)x+3k+3=0(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像都经过点A(2,m).
的图像都经过点A(2,m).
(1)求反比例函数的解析式;
(2)点B在![]() 轴的上,且OA=BA,反比例函数图像上有一点C,且∠ABC=90°,求点C坐标.
轴的上,且OA=BA,反比例函数图像上有一点C,且∠ABC=90°,求点C坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com