
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.
(1)当点E是BD的中点时,求tan∠AFB的值;
(2)CE•AF的值是否随线段AD长度的改变而变化?如果不变,求出CE•AF的值;如果变化,请说明理由;
(3)当△BGE和△BAF相似时,求线段AF的长.


【考点】相似形综合题;全等三角形的判定与性质;三角形中位线定理;正方形的判定与性质;圆的综合题;锐角三角函数的定义;特殊角的三角函数值.
【专题】综合题.
【分析】(1)过点E作EH⊥CD于H,如图1,易证EH是△DBC的中位线及△AHE∽△EHD,设AH=x,运用相似三角形的性质可求出x,就可求出tan∠AFB的值;
(2)取AB的中点O,连接OC、OE,如图2,易证四点A、C、B、E共圆,根据圆周角定理可得∠BCE=∠BAF,根据圆内接四边形内角互补可得∠CBE+∠CAE=180°,由此可推出∠CBE=∠BFA,从而可得△BCE∽△FAB,即可得到CE•FA=BC•AB,只需求出AB就可解决问题;
(3)过点E作EH⊥CD于H,作EM⊥BC于M,如图3,易证四边形EMCH是矩形,由△BCE∽△FAB,△BGE与△FAB相似可得△BGE与△BCE相似,即可得到∠EBG=∠ECB.由点A、C、B、E共圆可得∠ECA=∠EBG,即可得到∠ECB=∠ECA,根据角平分线的性质可得EM=EH,即可得到矩形EMCH是正方形,则有CM=CH,易证EB=EA,根据HL可得Rt△BME∽Rt△AHE,则有BM=AH.设AH=x,根据CM=CH可求出x,由此可求出CE的长,再利用(2)中的结果就可求出AF的值.
【解答】解:(1)过点E作EH⊥CD于H,如图1,
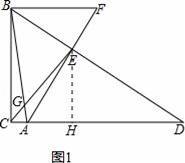

则有∠EHA=∠EHD=90°.
∵∠BCD=90°,BE=DE,
∴CE=DE.
∴CH=DH,
∴EH=
 BC=
BC=
 .
.
设AH=x,则DH=CH=x+1.
∵AE⊥BD,
∴∠AEH+∠DEH=∠AED=90°.
∵∠AEH+∠EAH=90°,
∴∠EAH=∠DEH,
∴△AHE∽△EHD,
∴
 =
=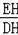
 ,
,
∴EH2=AH•DH,
∴(
 )2=x(x+1),
)2=x(x+1),
解得x=
 (舍负),
(舍负),
∴tan∠EAH=
 =
=
 =
=
 .
.
∵BF∥CD,
∴∠AFB=∠EAH,
∴tan∠AFB=
 ;
;
(2)CE•AF的值不变.
取AB的中点O,连接OC、OE,如图2,
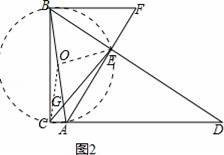

∵∠BCA=∠BEA=90°,
∴OC=OA=OB=OE,
∴点A、C、B、E共圆,
∴∠BCE=∠BAF,∠CBE+∠CAE=180°.
∵BF∥CD,
∴∠BFA+∠CAE=180°,
∴∠CBE=∠BFA,
∴△BCE∽△FAB,
∴
 =
=
 ,
,
∴CE•FA=BC•AB.
∵∠BCA=90°,BC=7,AC=1,
∴AB=5
 ,
,
∴CE•FA=7×5
 =35
=35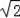
 ;
;
(3)过点E作EH⊥CD于H,作EM⊥BC于M,如图3,


∴∠EMC=∠MCH=∠CHE=90°,
∴四边形EMCH是矩形.
∵△BCE∽△FAB,△BGE与△FAB相似,
∴△BGE与△BCE相似,
∴∠EBG=∠ECB.
∵点A、C、B、E共圆,
∴∠ECA=∠EBG,
∴∠ECB=∠ECA,
∴EM=EH,
∴矩形EMCH是正方形,
∴CM=CH.
∵∠ECB=∠ECA=
 ∠BCA=45°,
∠BCA=45°,
∴∠EBA=∠EAB=45°,
∴EB=EA,
∴Rt△BME≌Rt△AHE(HL),
∴BM=AH.
设AH=x,则BM=x,CM=7﹣x,CH=1+x,
∴7﹣x=1+x,
∴x=3,
∴CH=4.
在Rt△CHE中,
cos∠ECH=
 =
=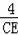
 =
=
 ,
,
∴CE=4
 .
.
由(2)可得CE•FA=35
 ,
,
∴AF=
 =
=
 .
.
【点评】本题主要考查了直角三角形斜边上的中线等于斜边的一半、等腰三角形的性质、三角形中位线定理、平行线的性质、相似三角形的判定与性质、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值、正方形的判定与性质等知识,综合性强,有一定的难度,证到△BCE∽△FAB是解决第(2)小题的关键,证出Rt△BME≌Rt△AHE是解决第(3)小题的关键.


科目:初中数学 来源: 题型:
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )


A.r B.2
 r C.
r C.
 r D.3r
r D.3r
查看答案和解析>>
科目:初中数学 来源: 题型:
若将30°、45°、60°的三角函数值填入表中,则从表中任意取一个值,是
 的概率为( )
的概率为( )
| α | 30° | 45° | 60° |
| sinα | |||
| cosα | |||
| tanα |
A.
 B.
B.
 C.
C.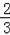
 D.
D.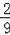

查看答案和解析>>
科目:初中数学 来源: 题型:
甲队修路150m与乙队修路120m所用天数相同,已知甲队比乙队每天多修10m,设甲队每天修路xm.依题意,下面所列方程正确的是( )
A.
 =
=
 B.
B.
 =
=
 C.
C.
 =
=
 D.
D.
 =
=

查看答案和解析>>
科目:初中数学 来源: 题型:
在下列以线段a、b、c的长为三边的三角形中,不能构成直角三角形的是( )
A、a=9,b=41,c=40 B、a=b=5,c=5
C、a∶b∶c=3∶4∶5 D、a=11,b=12,c=15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com