
分析 设小明步行的速度为x千米/时,则公交车的速度为9x千米/时,小明共步行了2千米,小明乘公共汽车行驶了36千米,则根据时间列方程得到$\frac{1.5+0.5}{x}$+$\frac{38-1.5-0.5}{9x}$=$\frac{90}{60}$,然后解方程、检验即可得到x的值.
解答 解:设小明步行的速度为x千米/时,则公交车的速度为9x千米/时,
根据题意得$\frac{1.5+0.5}{x}$+$\frac{38-1.5-0.5}{9x}$=$\frac{90}{60}$,
解得x=4,
经检验x=4是原方程的解.
答:小明步行的速度为4千米/时.
点评 本题考查了分式方程的应用:列分式方程解应用题的一般步骤:设、列、解、验、答.必须严格按照这5步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.要掌握常见问题中的基本关系,如行程问题:速度=路程时间;工作量问题:工作效率=工作量工作时间等等.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:填空题
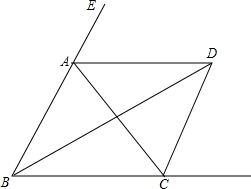 如图所示,在△ABC中,AB=AC,∠EAC和∠FCA均是△ABC的外角,BD平分∠ABC,AD平分∠EAC,CD平分∠ACF,现有以下结论:①AD∥BC;②∠ADC+∠ABD=90°;③∠BDC=$\frac{1}{2}$∠BAC,其中正确的结论有①②③.
如图所示,在△ABC中,AB=AC,∠EAC和∠FCA均是△ABC的外角,BD平分∠ABC,AD平分∠EAC,CD平分∠ACF,现有以下结论:①AD∥BC;②∠ADC+∠ABD=90°;③∠BDC=$\frac{1}{2}$∠BAC,其中正确的结论有①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com