Question

2．有一块直角三角形的绿地，量得两直角边长分别为6m，8m
（1）求斜边的长；
（2）求斜边上的高；
（3）现在要将绿地扩充成等腰三角形，且扩充部分是以8m为直角边的直角三角形，求扩充后等腰三角形绿地的周长．

Answer 1

分析 （1）直接利用勾股定理可得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{36+64}$=10；
（2）首先作出图形，再利用直角三角形的面积可得$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB×CD，代入数进行计算即可；
（3）此题要分三种情况，分别画出图形，然后求周长即可．

解答 解：（1）如图所示：∵AC=8m，BC=6m，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{36+64}$=10（m）；

（2）过C作CD⊥AB，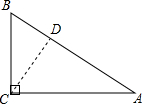

∵S_△ACB=$\frac{1}{2}$AC•BC，S_△ACB=$\frac{1}{2}$AB×CD，
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB×CD，
∴$\frac{1}{2}×6×8$=$\frac{1}{2}×10×CD$，
CD=4.8m；

（3）如图①所示：等腰三角形绿地的周长：6+6+10+10=32（m）；

如图②所示：AE=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$（m），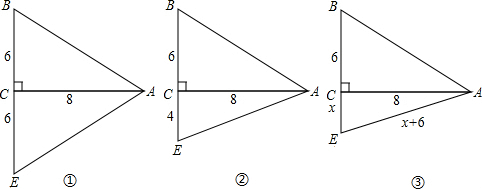
等腰三角形绿地的周长：4+6+10+4$\sqrt{5}$=20+4$\sqrt{5}$（m）；

如图③所示：在Rt△ACD中，AC²+EC²=AE²，
即8²+x²=（x+6）²，
解得：x=$\frac{7}{3}$，
等腰三角形绿地的周长：6+$\frac{7}{3}$+6$+\frac{7}{3}$+10=26$\frac{2}{3}$（m），
答：扩充后等腰三角形绿地的周长为32m或（20+4$\sqrt{5}$）m或26$\frac{2}{3}$m．

点评 此题主要考查了勾股定理的应用，以及等腰三角形，关键是正确作出图形，不要漏解．