
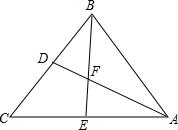
 如图,△ABC的中线为AD,BE相交于点F,若△ABC的面积是45,求四边形DCEF的面积.
如图,△ABC的中线为AD,BE相交于点F,若△ABC的面积是45,求四边形DCEF的面积.| 1 |
| 2 |
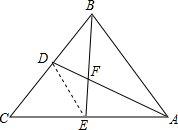
| 1 |
| 2 |
| 45 |
| S△CDE |
| DE |
| AB |
| EF |
| BF |
| DF |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| DE |
| AB |
| EF |
| BF |
| DF |
| AF |
| 1 |
| 2 |
| 1 |
| 4 |


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
| 甲种原料x克 | 乙种原料y克 | 所配置的营养品 | |
| 所含蛋白质(单位) | 0.5x | ||
| 所含铁质(单位) | 0.4y |
查看答案和解析>>
科目:初中数学 来源: 题型:
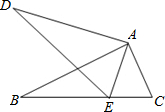 如图,在△ABC和△ADE中,点E在BC上,∠BAC=∠DAE,∠B=∠D,AB=AD,
如图,在△ABC和△ADE中,点E在BC上,∠BAC=∠DAE,∠B=∠D,AB=AD,查看答案和解析>>
科目:初中数学 来源: 题型:
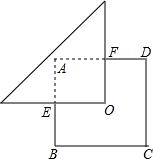 如图,O是边长为a的正方形ABCD的中心,将一块腰长足够长的等腰直角三角形纸板的直角顶点放在O处,并将纸板绕O点旋转.问正方形被纸板覆盖部分的面积是否发生变化.请说明理由.
如图,O是边长为a的正方形ABCD的中心,将一块腰长足够长的等腰直角三角形纸板的直角顶点放在O处,并将纸板绕O点旋转.问正方形被纸板覆盖部分的面积是否发生变化.请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com