练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知某开发区有一块四边形空地ABCD，现计划在该空地上种植草皮，经测量∠ADC=90°，CD=6m，AD=8m，BC=24cm，AB=26m，若每平方米草皮需200元，则在该空地上种植草皮共需多少钱？

    【答案】19200

    【解析】

    连接AC，在Rt△ACD中，根据勾股定理求出AC2,由于AC2+BC2=AB2根据勾股定理的逆定理求出∠ACB=90°，由S四边形ABCD=S△ACB-S△ACD可得最终结果.

    解：连接AC，


    在Rt△ACD中，AC2=CD2+AD2=62+82=102，
    在△ABC中，AB2=262，BC2=242，
    而102+242=262，
    即AC2+BC2=AB2，
    ∴∠ACB=90°，
    S四边形ABCD=S△ACB-S△ACD=ACBC-ADCD，
    =×10×24-×8×6=96．
    所以需费用96×200=19200（元）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ACB=90°，AC=BC，D为BC中点，CE⊥AD于E，BF∥AC交CE的延长线于F．

    （1）求证：△ACD≌△CBF；

    （2）求证：AB垂直平分DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂拟建一座平面图形为矩形且面积为平方米的三级污水处理池（平面图如图所示）．由于地形限制，三级污水处理池的长、宽都不能超过米．如果池的外围墙建造单价为每米元，中间两条隔墙建造单价为每米元，池底建造单价为每平方米元．（池墙的厚度忽略不计）

    当三级污水处理池的总造价为元时，求池长；

    如果规定总造价越低就越合算，那么根据题目提供的信息，以元为总造价来修建三级污水处理池是否最合算？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中，以线段为边作，使得，连接，再以为边作，使得，．

    （）如图1，连结，求证：．

    （）如图2，时，将线段沿着射线的方向平移，得到线段，连接，．

    ①若，依题意补全图2，求线段的长．

    ②请直接写出线段的长（用含的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形OCED的周长为（　　）

    A. 4 B. 8 C. 10 D. 12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形AOBC中，点A的坐标是（﹣2，1），点C的纵坐标是4，则B、C两点的坐标分别是 （ ）

    A. （，3）、（﹣，4） B. （，3）、（﹣，4）

    C. （，）、（﹣，4） D. （，）、（﹣，4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是等边三角形，，分别是，的中点，且.是上一动点，则的最小值为___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直角梯形ABCD中，∠C=∠D=90°，AD＜BC，BC=CD=6，E是边CD上的一点，恰好使AE=5，并且∠ABE=45°，则CE的长是___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

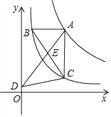
    【题目】如图，点A是反比例函数y=图象上的任意一点，过点A作AB∥x轴，AC∥y轴，分别交反比例函数y=的图象于点B，C，连接BC，E是BC上一点，连接并延长AE交y轴于点D，连接CD，则S△DEC﹣S△BEA=_________．

    查看答案和解析>>

    同步练习册答案