
 要求tan45°的值,可构造直角三角形进行计算,如图所示,作Rt△ABC,使∠C=90°,直角边AC=BC=1,斜边AB=$\sqrt{2}$.∠ABC=45°,所以tan45°=$\frac{AC}{BC}$=$\frac{1}{1}$=1.
要求tan45°的值,可构造直角三角形进行计算,如图所示,作Rt△ABC,使∠C=90°,直角边AC=BC=1,斜边AB=$\sqrt{2}$.∠ABC=45°,所以tan45°=$\frac{AC}{BC}$=$\frac{1}{1}$=1.分析 (1)延长CA到D,使DA=AC,连结DB,如图1,Rt△ABC,∠C=90°,AC=BC=1,AB=$\sqrt{2}$.∠ABC=45°,根据等腰三角形的性质和三角形外角性质可计算出∠D=22.5°,然后在Rt△BDC中,根据正切的定义可求出tan22.5°的值;
(2)Rt△ABC,∠C=90°,AC=$\sqrt{3}$,BC=1,AB=2,∠BAC=30°,延长CA到D,使AD=AB=2,根据等腰三角形的性质和三角形外角性质可计算出∠D=15°,然后在Rt△BDC中,根据正切的定义可求出tan15°的值.
解答 解:(1)延长CA到D,使DA=AC,连结DB,如图1,
Rt△ABC,∠C=90°,AC=BC=1,AB=$\sqrt{2}$.∠ABC=45°,
∵AD=AB=$\sqrt{2}$,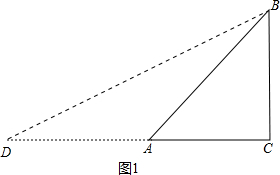
∴∠D=∠ABD,
而∠BAC=∠D+∠ABD=45°,
∴∠D=22.5°,
在Rt△BDC中,tanD=$\frac{BC}{DC}$=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,
即tan22.5°=$\sqrt{2}$-1;
(2)Rt△ABC,∠C=90°,AC=$\sqrt{3}$,BC=1,AB=2,∠BAC=30°,延长CA到D,使AD=AB=2,
∵AD=AB=$\sqrt{2}$,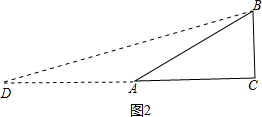
∴∠D=∠ABD,
而∠BAC=∠D+∠ABD=30°,
∴∠D=15°,
在Rt△BDC中,tanD=$\frac{BC}{DC}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,
即tan15°=2-$\sqrt{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活运用勾股定理和锐角三角函数的定义.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017届辽宁省大石桥市中考模拟(一)数学试卷(解析版) 题型:判断题
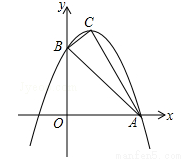
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
为了了解一批产品的质量,从中抽取300个产品进行检验,在这个问题中,被抽取的300个产品叫做( )
A. 总体 B. 个体 C. 总体的一个样本 D. 普查方式
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
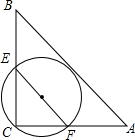 如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )
如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )| A. | 2.4 | B. | 2 | C. | 2.5 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
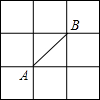 在如图所示的正方形网格中,网线的交点叫做格点.已知A,B是格点,请在图中找格点C,使△ABC是等腰三角形.这样的格点个数有( )
在如图所示的正方形网格中,网线的交点叫做格点.已知A,B是格点,请在图中找格点C,使△ABC是等腰三角形.这样的格点个数有( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com