
【题目】如图是一种新型娱乐设施的示意图,x轴所在位置记为地面,平台AB∥x轴,OA=6米,AB=2米,BC是反比例函数y= ![]() 的图象的一部分,CD是二次函数y=﹣x2+mx+n图象的一部分,连接点C为抛物线的顶点,且C点到地面的距离为2米,D点是娱乐设施与地面的一个接触点.
的图象的一部分,CD是二次函数y=﹣x2+mx+n图象的一部分,连接点C为抛物线的顶点,且C点到地面的距离为2米,D点是娱乐设施与地面的一个接触点. 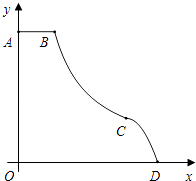
(1)试求k,m,n的值;
(2)试求点B与点D的水平距离.
【答案】
(1)解:把B(2,6)代入y= ![]() ,可得y=
,可得y= ![]() ,
,
把y=2代入y= ![]() ,可得x=6,即C点坐标为(6,2).
,可得x=6,即C点坐标为(6,2).
∵二次函数y=﹣x2+mx+n的顶点为C,
∴y=﹣(x﹣6)2+2,
∴y=﹣x2+12x﹣34.
∴k=12,m=12,n=﹣34
(2)解:把y=0代入y=﹣(x﹣6)2+2,解得:x1=6+ ![]() ,x2=6﹣
,x2=6﹣ ![]() .
.
故点B与点D的距离为6+ ![]() ﹣2=4+
﹣2=4+ ![]()
【解析】(1)把B(2,6)代入y= ![]() ,可得y=
,可得y= ![]() ,把y=2代入y=
,把y=2代入y= ![]() ,于是求得C点坐标为(6,2).由于二次函数y=﹣x2+mx+n的顶点为C,于是得到y=﹣(x﹣6)2+2,即可得到结论;(2)把y=0代入y=﹣(x﹣6)2+2,求得x1=6+
,于是求得C点坐标为(6,2).由于二次函数y=﹣x2+mx+n的顶点为C,于是得到y=﹣(x﹣6)2+2,即可得到结论;(2)把y=0代入y=﹣(x﹣6)2+2,求得x1=6+ ![]() ,x2=6﹣
,x2=6﹣ ![]() .即可得到结论.
.即可得到结论.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】(1)探究规律:如图,已知□ABCD,试用三种方法将它分成面积相等的两部分:



(2)解决问题:兄弟俩共同承包的一块平行四边形的土地,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了,聪明的你能帮他们解决这个问题吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式:![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…![]() ,
,![]() ,…写出第
,…写出第![]() 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路.
![]() 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么?
![]() 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么?
![]() 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第![]() 个单项式是什么?
个单项式是什么?
![]() 请你根据猜想,请写出第
请你根据猜想,请写出第![]() 个,第
个,第![]() 个单项式.
个单项式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题: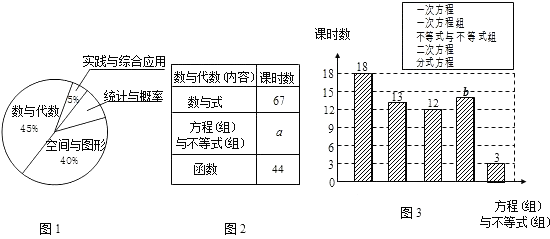
(1)图1中“统计与概率”所在扇形的圆心角为度;
(2)图2、3中的a= , b=;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)某自行车厂一周计划生产700辆自行车,平均每天生产自行车100辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
(1)根据记录可知前三天共生产自行车 辆;
(2)产量最多的一天比产量最少的一天生产 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制。如果每生产一辆自行车就可以得人民币60 元,超额完多成任务,每超一辆可多得 15 元;若不足计划数的,每少生产一辆扣 15 元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式:a1=![]() =
=![]() -
-![]()
第二个等式:a2= =
=![]() -
-![]()
第三个等式:a3= =
=![]() -
-![]()
第四个等式:a4= =
=![]() -
-![]()
按上述规律,回答下列问题:
(1)请写出第六个等式:a6=_____=_____;
(2)用含n的代数式表示第n个等式:an=_____=_____;
(3)a1+a2+a3+a4+a5+a6=_____(得出最简结果);
(4)计算:a1+a2+…+an.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com