
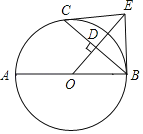
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.
(1)求证:BE与⊙O相切;
(2)若OD=DE,AB=6,求由![]() ,线段BC,AB所围成图形的面积.
,线段BC,AB所围成图形的面积.
【答案】(1)详见解析;(2)![]() π+
π+![]() .
.
【解析】
(1)连接OC,易证得△COE≌△BOE(SAS),即可得∠OCE=∠OBE=90°,证得BE与⊙O相切;
(2)根据切线的性质得到CE=BE,推出四边形OBEC是正方形,得到∠BOC=90°,根据平角的定义得到∠AOC=90°,根据扇形和三角形的面积公式即可得到结论.
(1)证明:连接OC,
∵CE是⊙O的切线,
∵OB=OC,OD⊥BC,
∴∠EOC=∠EOB,
∵在△EOC和△EOB中,,
∴△COE≌△BOE(SAS),
∴∠OCE=∠OBE=90°,
即OB⊥BE,
∴BE与⊙O相切;
(2)解:∵CE,BE是⊙O的切线,
∴CE=BE,
∵OE⊥BC,OD=DE,
∴OC=CE,OB=BE,
∴OC=OB=BE=CE,
∴四边形OBEC是菱形,
∵∠OBE=90°,
∴四边形OBEC是正方形,
∴∠BOC=90°,
∴∠AOC=90°,
∵AB=6,
∴AO=OC=OB=3,
∴由![]() ,线段BC,AB所围成图形的面积=S扇形AOC+S△BCO=
,线段BC,AB所围成图形的面积=S扇形AOC+S△BCO=![]() +
+![]() ×3×3=
×3×3=![]() π+
π+![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中.

(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标;
三个顶点的坐标;
(2)直接写出△ABC的面积为 ;
(3)在x轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面![]() m,则水流落地点B离墙的距离OB是( )
m,则水流落地点B离墙的距离OB是( )
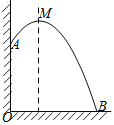
A.2mB.3mC.4mD.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
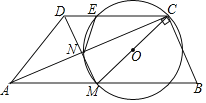
【题目】如图,在Rt△ABC中,M是斜边AB的中点,以CM为直径作圆O交AC于点N,延长MN至D,使ND=MN,连接AD、CD,CD交圆O于点E.
(1)判断四边形AMCD的形状,并说明理由;
(2)求证:ND=NE;
(3)若DE=2,EC=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小刚家,菜地,稻田在同一条直线上.小刚从家去菜地浇水,又去稻田除草,然后回家.如图反映了这个过程中,小刚离家的距离y与时间x之间的对应关系.如果菜地和稻田的距离为akm,小刚在稻田除草比在菜地浇水多用了bmin,则a,b的值分别为( )
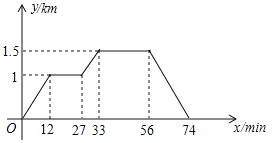
A.1,8B.0.5,12C.1,12D.0.5,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
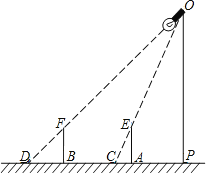
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:其中,正确的个数有( )
①b2﹣4ac<0;②a﹣b+c<0;③abc>0;④m>﹣2.
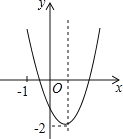
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个阳光明媚的上午,小明和小兰相约从鲁能巴蜀中学沿相同的路线去龙头寺公园写生,小明出发5分钟后小兰才出发,此时小明发现忘记带颜料,立即按原速原路回学校拿颜料,小明拿到颜料后,以比原速提髙20%的速度赶去公园,结果还是比小兰晚2分钟到公园(小明拿颜料的时间忽略不计).在整个过程中,小兰保持匀速运动,小明提速前后也分别保持匀速运动,如图所示是小明与小兰之间的距离![]() (米)与小明出发的时间
(米)与小明出发的时间![]() (分钟)之间的函数图象,则学校到公园的距离为_______米.
(分钟)之间的函数图象,则学校到公园的距离为_______米.
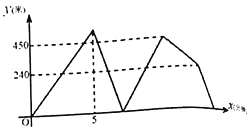
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻落实省教育厅提出的“三生教育”.在母亲节来临之际,某校团委组织了以“珍爱生命,
学会生存,感恩父母”为主题的教育活动,在学校随机调查了50名同学平均每周在家做家务的时间,统
计并制作了如下的频数分布表和扇形统计图:
组别 | 做家务的时间 | 频数 | 频率 |
A | 1≤t<2 | 3 | 0.06 |
B | 2≤t<4 | 20 | 0.40 |
C | 4≤t<6 | a | 0.30 |
D | 6≤t<8 | 8 | b |
E | t≥8 | 4 | 0.08 |
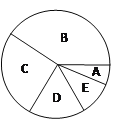
根据上述信息回答下列问题:
(1)a= ,b= .
(2)在扇形统计图中,B组所占圆心角的度数为 .
(3)全校共有2000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com