
【题目】已知直线l的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() ,圆C的参数方程为:
,圆C的参数方程为: ![]() (其中θ为参数).
(其中θ为参数).
(1)判断直线l与圆C的位置关系;
(2)若椭圆的参数方程为 ![]() (φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|.
(φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|.
【答案】
(1)解:将直线l的极坐标方程 ![]() ,化为直角坐标方程:x+y﹣1=0.
,化为直角坐标方程:x+y﹣1=0.
将圆C的参数方程化为普通方程:x2+(y+2)2=4,圆心为C(0,﹣2),半径r=2.
∴圆心C到直线l的距离为d= ![]() >r=2,
>r=2,
∴直线l与圆C相离.
(2)解:将椭圆的参数方程化为普通方程为 ![]() ,
,
∵直线l:x+y﹣1=0的斜率为k1=﹣1,
∴直线l'的斜率为k2=1,即倾斜角为 ![]() ,
,
则直线l'的参数方程为 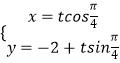 ,(t为参数),
,(t为参数),
即 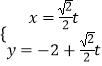 (t为参数),
(t为参数),
把直线l'的参数方程 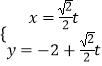 代入
代入 ![]() ,
,
整理得7t2﹣16 ![]() t+8=0.(*)
t+8=0.(*)
由于△=(﹣16 ![]() )2﹣4×7×8>0,
)2﹣4×7×8>0,
故可设t1,t2是方程(*)的两个不等实根,则有t1t2= ![]() ,
, ![]() ,
,
|AB|= ![]()
【解析】(1)将直线l的极坐标方程化为直角坐标方程,将圆C的参数方程化为普通方程,求出圆心C到直线l的距离,由此得到直线l与圆C相离.(2)将椭圆的参数方程化为普通方程为 ![]() ,求出直线l'的参数方程,把直线l'的参数方程代入椭圆的普通方程,得7t2﹣16
,求出直线l'的参数方程,把直线l'的参数方程代入椭圆的普通方程,得7t2﹣16 ![]() t+8=0,由此利用根的判别式、韦达定理、弦长公式能求出|AB|.
t+8=0,由此利用根的判别式、韦达定理、弦长公式能求出|AB|.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 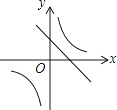
A.
B.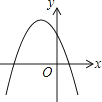
C.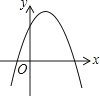
D.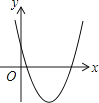
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据某市地产数据研究院的数据显示,2016年该市新建住宅销售均价走势如图所示,为抑制房价过快上涨,政府从8月份采取宏观调控措施,10月份开始房价得到很好的抑制. 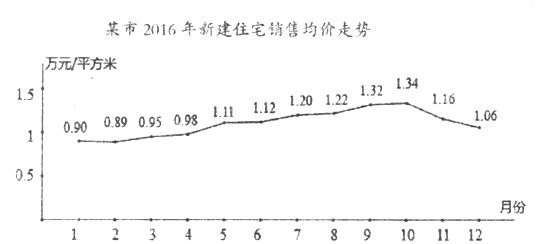
(Ⅰ)地产数据研究院研究发现,3月至7月的各月均价y(万元/平方米)与月份x之间具有较强的线性相关关系,试建立y关于x的回归方程(系数精确到0.01),政府若不调控,依次相关关系预测第12月份该市新建住宅销售均价;
(Ⅱ)地产数据研究院在2016年的12个月份中,随机抽取三个月份的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为X,求X的分布列和数学期望.
参考数据: ![]() =25,
=25, ![]() =5.36,
=5.36, ![]() =0.64
=0.64
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:![]() =
= 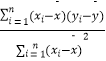 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知向量 ![]() ,向量
,向量 ![]() 如图表示,则( )
如图表示,则( ) 
A.?λ>0,使得 ![]()
B.?λ>0,使得< ![]() ,
, ![]() >=60°
>=60°
C.?λ<0,使得< ![]() ,
, ![]() >=30°
>=30°
D.?λ>0,使得 ![]() 为不为0的常数)
为不为0的常数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com