
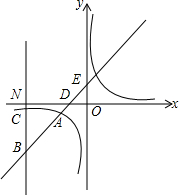
 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y=| m |
| x |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| m |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 18 |
| 5 |
| 1 |
| 2 |
| 18 |
| 5 |
| 27 |
| 5 |


科目:初中数学 来源: 题型:
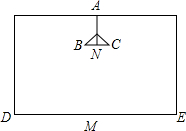 在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8m,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,
在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8m,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点.
如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com