
【题目】抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
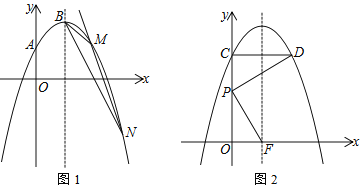
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
【答案】(1)y=﹣x2+2x+1;(2)-3;(3)当m=2![]() ﹣1时,点P的坐标为(0,
﹣1时,点P的坐标为(0,![]() )和(0,
)和(0,![]() );当m=2时,点P的坐标为(0,1)和(0,2).
);当m=2时,点P的坐标为(0,1)和(0,2).
【解析】
(1)根据对称轴为直线x=1且抛物线过点A(0,1)利用待定系数法进行求解可即得;
(2)根据直线y=kx﹣k+4=k(x﹣1)+4知直线所过定点G坐标为(1,4),从而得出BG=2,由S△BMN=S△BNG﹣S△BMG=![]() BGxN﹣
BGxN﹣![]() BGxM=1得出xN﹣xM=1,联立直线和抛物线解析式求得x=
BGxM=1得出xN﹣xM=1,联立直线和抛物线解析式求得x=![]() ,根据xN﹣xM=1列出关于k的方程,解之可得;
,根据xN﹣xM=1列出关于k的方程,解之可得;
(3)设抛物线L1的解析式为y=﹣x2+2x+1+m,知C(0,1+m)、D(2,1+m)、F(1,0),再设P(0,t),分△PCD∽△POF和△PCD∽△POF两种情况,由对应边成比例得出关于t与m的方程,利用符合条件的点P恰有2个,结合方程的解的情况求解可得.
(1)由题意知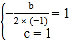 ,解得:
,解得:![]() ,
,
∴抛物线L的解析式为y=﹣x2+2x+1;
(2)如图1,设M点的横坐标为xM,N点的横坐标为xN,
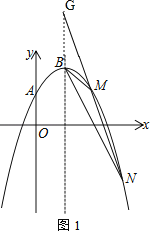
∵y=kx﹣k+4=k(x﹣1)+4,
∴当x=1时,y=4,即该直线所过定点G坐标为(1,4),
∵y=﹣x2+2x+1=﹣(x﹣1)2+2,
∴点B(1,2),
则BG=2,
∵S△BMN=1,即S△BNG﹣S△BMG=![]() BG(xN﹣1)-
BG(xN﹣1)-![]() BG(xM-1)=1,
BG(xM-1)=1,
∴xN﹣xM=1,
由![]() 得:x2+(k﹣2)x﹣k+3=0,
得:x2+(k﹣2)x﹣k+3=0,
解得:x=![]() =
=![]() ,
,
则xN=![]() 、xM=
、xM=![]() ,
,
由xN﹣xM=1得![]() =1,
=1,
∴k=±3,
∵k<0,
∴k=﹣3;
(3)如图2,

设抛物线L1的解析式为y=﹣x2+2x+1+m,
∴C(0,1+m)、D(2,1+m)、F(1,0),
设P(0,t),
(a)当△PCD∽△FOP时,![]() ,
,
∴![]() ,
,
∴t2﹣(1+m)t+2=0①;
(b)当△PCD∽△POF时,![]() ,
,
∴![]() ,
,
∴t=![]() (m+1)②;
(m+1)②;
(Ⅰ)当方程①有两个相等实数根时,
△=(1+m)2﹣8=0,
解得:m=2![]() ﹣1(负值舍去),
﹣1(负值舍去),
此时方程①有两个相等实数根t1=t2=![]() ,
,
方程②有一个实数根t=![]() ,
,
∴m=2![]() ﹣1,
﹣1,
此时点P的坐标为(0,![]() )和(0,
)和(0,![]() );
);
(Ⅱ)当方程①有两个不相等的实数根时,
把②代入①,得:![]() (m+1)2﹣
(m+1)2﹣![]() (m+1)+2=0,
(m+1)+2=0,
解得:m=2(负值舍去),
此时,方程①有两个不相等的实数根t1=1、t2=2,
方程②有一个实数根t=1,
∴m=2,此时点P的坐标为(0,1)和(0,2);
综上,当m=2![]() ﹣1时,点P的坐标为(0,
﹣1时,点P的坐标为(0,![]() )和(0,
)和(0,![]() );
);
当m=2时,点P的坐标为(0,1)和(0,2).


科目:初中数学 来源: 题型:
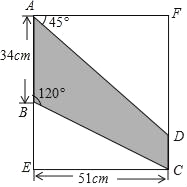
【题目】小明准备用一块矩形材料剪出如图所示的四边形ABCD(阴影部分),作为要制作的风筝的一个翅膀,请你根据图中的数据帮小明计算出CD的长度.(结果精确到0.1cm)(参考数据:sin60°=0.87,cos60°=0.50,tan60°=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
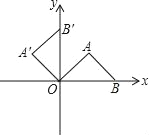
【题目】在直角坐标系中,等腰直角三角形AOB在如图所示的位置,点B的横坐标为2,将△AOB绕点O按逆时针方向旋转90°,得到△A′OB′,则点A′的坐标为( )
A. (1,1) B. (![]() ,
,![]() )
)
C. (﹣1,1) D. (﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
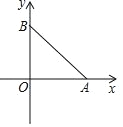
查看答案和解析>>
科目:初中数学 来源: 题型:
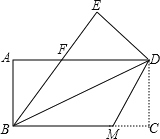
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
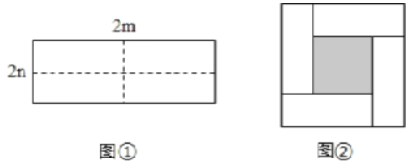
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:![]() ;
;
方法二:![]() .
.
(2)(m+n)![]() ,(mn)
,(mn) ![]() ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com