
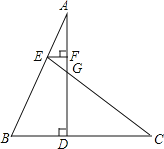
【题目】如图,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5cm,BE=10cm,BD=9cm,CD=5cm,求AF、FG、GD的长.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
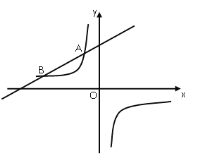
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点P是边AC上一点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,BD平分∠ABC,以下四个结论①△BQD是等腰三角形;②BQ=DP;③PA=![]() QP;④
QP;④![]() =(1+
=(1+![]() )2;其中正确的结论的个数( )
)2;其中正确的结论的个数( )
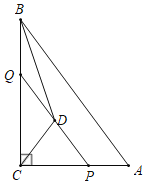
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:
(1)求y与x的函数解析式(也称关系式);
(2)求这一天销售西瓜获得的利润的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元,经调查发现每天的销售量![]() (个
(个![]() 与每个商品的售价
与每个商品的售价![]() (元
(元![]() 满足一次函数关系,其部分数据如下所示:
满足一次函数关系,其部分数据如下所示:
每个商品的售价 |
| 30 | 40 | 50 |
|
每天销售量 |
| 100 | 80 | 60 |
|
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出10件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出1件,若商场平均每天要盈利600元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
科目:初中数学 来源: 题型:
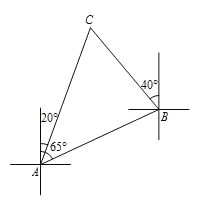
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
![]() 他们在一次实验中共掷骰子
他们在一次实验中共掷骰子![]() 次,试验的结果如下:
次,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最大.”她的说法正确吗?为什么?
点朝上的概率最大.”她的说法正确吗?为什么?
![]() 小颖和小红在实验中如果各掷一枚骰子,那么枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
小颖和小红在实验中如果各掷一枚骰子,那么枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com