
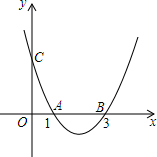
 (1)已知二次函数y=(x-1)(x-3)的图象如图,请根据图象直接写出该二次函数图象经过怎样的左右平移,新图象通过坐标原点?
(1)已知二次函数y=(x-1)(x-3)的图象如图,请根据图象直接写出该二次函数图象经过怎样的左右平移,新图象通过坐标原点?分析 (1)首先求得抛物线与x轴的交点,即可求得平移的方向和距离;
(2)根据“a、c相反,b不变”,即可求得对应的函数解析式,然后确定顶点即可判断;
(3)△MAB中M是在抛物线的对称轴上,则△MAB为等腰三角形,则△NBC是等腰三角形,同时根据∠OBC=45°,即已知等腰△NBC的一个角的度数,据此即可讨论,求解;
(4)设E的坐标是(a,a2-4a+3),由点E与F关于点D($\frac{3}{2}$,0)对称,则可得F的坐标,然后根据点E和点F的纵坐标互为相反数即可列方程求解.
解答 解:(1)二次函数y=(x-1)(x-3)与x轴的交点是(1,0)和(3,0).
抛物线向左平移1个单位长度或3个单位长度即可使新图象经过坐标原点;
(2)y=(x-1)(x-3)=x2-4x+3.
∵小胡同学听成了a与c相反,b不变.
∴y=-x2-4x-3=-(x+2)2+1,顶点坐标是(-2,1),
故与原抛物线关于原点对称;
(3)∵△MAB中M是在抛物线的对称轴上,
∴MA=MB,即△MAB为等腰三角形,
又∵△MAB与△NBC相似,
∴△NBC是等腰三角形.
∵N在x轴上,
∴∠CBN=45°或135°.
当∠CBN=135°时,即N点在B的右侧且BC=BN,则N的坐标是(3+3$\sqrt{2}$,0);
当∠CBN=45°时,即N在点B的左侧,
若△MAB的底角为45°,此时三角形为等腰直角三角形,则N的坐标是(0,0)或(-3,0);
若△MAB的顶角是45°时,在△NBC中,BC=BN=3$\sqrt{2}$,则N的坐标是(3-3$\sqrt{2}$,0);
(4)设E的坐标是(a,a2-4a+3),
由点E与F关于点D($\frac{3}{2}$,0)对称,则可得F(3-a,a2-2a),
∴点E和点F的纵坐标互为相反数,即a2-4a+3+a2-2a=0,
解得:a1=$\frac{3-\sqrt{3}}{2}$,a2=$\frac{3+\sqrt{3}}{2}$(舍去),
∴E的纵坐标是($\frac{3-\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$),F的坐标是($\frac{3+\sqrt{3}}{2}$,-$\frac{\sqrt{3}}{2}$).
点评 本题考查了二次函数与等腰三角形的性质,相似三角形的性质,正确理解△NBC是等腰三角形是本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 明天一定会下雨 | |
| B. | 抛掷一枚均匀硬币,落地后正面朝上 | |
| C. | 任取两个正数,其和大于零 | |
| D. | 直角三角形的两锐角分别是20°和60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 76°46′ | B. | 76°86′ | C. | 86°56′ | D. | 166°46′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一种新型娱乐设施的示意图,x轴所在位置记为地面,平台AB∥x轴,OA=6米,AB=2米,BC是反比例函数y=$\frac{k}{x}$的图象的一部分,CD是二次函数y=-x2+mx+n图象的一部分,连接点C为抛物线的顶点,且C点到地面的距离为2米,D点是娱乐设施与地面的一个接触点.
如图是一种新型娱乐设施的示意图,x轴所在位置记为地面,平台AB∥x轴,OA=6米,AB=2米,BC是反比例函数y=$\frac{k}{x}$的图象的一部分,CD是二次函数y=-x2+mx+n图象的一部分,连接点C为抛物线的顶点,且C点到地面的距离为2米,D点是娱乐设施与地面的一个接触点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}(x+1)=3$ | B. | $\frac{1}{2}x+1=3$ | C. | 2x+1=3 | D. | 2(x+1)=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,有一个边长为20cm的正方形洞口,想用一个圆盖去盖住这个洞口,则圆盖的直径(结果保留整数)至少是( )
如图,有一个边长为20cm的正方形洞口,想用一个圆盖去盖住这个洞口,则圆盖的直径(结果保留整数)至少是( )| A. | 20cm | B. | 28cm | C. | 29cm | D. | 40cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.
如图,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com