

���� ��1������DC��x��ɵõ���C����������ڵ�D�������ֻ꣬�������D�����꣬�Ϳɵõ���C�������꣬Ȼ��ѵ�C�����������ֱ��CE�ı���ʽ���Ϳ������C�����ꣻ
��2�����M��ֱ��CE���е�ΪH������MH��M0������Բ�����ߵ����ʿɵ�MH��CE������M��x��Ĵ��߽�x����N����ֱ��DC��G����ͼ1��ֻ������������Ϳɽ�����⣻
��3������P��x��Ĵ��ߣ���DC��S��������R��ֱ��y���ֱ����T����ͼ2����R�������Ϊ��x��y����������ɵõ���P��Q�����꣨��t�Ĵ���ʽ��ʾ������֤��QSP�ա�PTR������SQ=PT��PS=RT���ɴ˿ɵõ���R�����꣨��t�Ĵ���ʽ��ʾ����Ȼ��ֻ��Ե�R�ֱ����ı���ABCD�ı����ڵ�ֱ���Ͻ������ۣ��Ϳɽ�����⣮
��� �⣺��1����x=0ʱ��y=3x+3=3����D��0��3����
��DC��x�ᣬ��yC=yD=3��
�ߵ�C��ֱ��y=$\frac{3}{4}$x�ϣ�
��3=$\frac{3}{4}$xC��
��xC=4��
��C��4��3����
�ʴ�Ϊ��4��3����
��2�����M��ֱ��CE���е�ΪH������MH��M0������MH��CE��
����M��x��Ĵ��߽�x����N����ֱ��DC��G����ͼ1��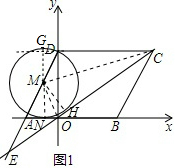
��ֱ��y=3x+3�ɵõ�A��-1��0����OA=1��
��AD���е�M����Ϊ��$\frac{-1+0}{2}$��$\frac{0+3}{2}$������-$\frac{1}{2}$��$\frac{3}{2}$����
��MN=$\frac{3}{2}$��MG=3-$\frac{3}{2}$=$\frac{3}{2}$��
��S��OMC=S����OADC-S��OAM-S��MDC��
��$\frac{1}{2}$OC•MH=$\frac{1}{2}$��DC+OA��•OD-$\frac{1}{2}$OA•MN-$\frac{1}{2}$DC•MG��
��$\frac{1}{2}$��$\sqrt{{4}^{2}+{3}^{2}}$•MH=$\frac{1}{2}$��4+1����3-$\frac{1}{2}$��1��$\frac{3}{2}$-$\frac{1}{2}$��4��$\frac{3}{2}$��
��MH=$\frac{3}{2}$��
���M�İ뾶Ϊ$\frac{3}{2}$��
��3��t=$\frac{5}{3}$��t=$\frac{20}{9}$��t=$\frac{35}{12}$��
��ʾ������P��x��Ĵ��ߣ���DC��S��������R��ֱ��y���ֱ����T����ͼ2��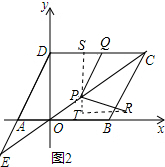
��R���������x��y����
����ɵ�CQ=OP=t������P��$\frac{4t}{5}$��$\frac{3t}{5}$����Q��4-t��3����
��֤��QSP�ա�PTR������SQ=PT��PS=RT��
��4-t-$\frac{4t}{5}$=$\frac{3t}{5}$-y��3-$\frac{3t}{5}$=x-$\frac{4t}{5}$��
��y=$\frac{12t}{5}$-4��x=$\frac{t}{5}$+3��
��R���������$\frac{t}{5}$+3��$\frac{12t}{5}$-4����
�ٵ���R��ֱ��AB��ʱ��$\frac{12t}{5}$-4=0�����t=$\frac{5}{3}$��
�ڵ���R��ֱ��BC��ʱ��
��BC��AD����y=3x+b���ѵ�C��4��3������ɵ�b=-9��
��ֱ��BC�ı���ʽΪy=3x-9��
��$\frac{12t}{5}$-4=3��$\frac{t}{5}$+3��-9��
���t=$\frac{20}{9}$��
�۵���R��ֱ��DC��ʱ��$\frac{12t}{5}$-4=3�����t=$\frac{35}{12}$��
�ܵ���R��ֱ��AD��ʱ��
�ɵ�$\frac{12t}{5}$-4=3��$\frac{t}{5}$+3��+3��
���t=$\frac{80}{9}$��
����ɵ�0��t��4��
��$\frac{80}{9}$��4������ȥ��
����������t=$\frac{5}{3}$��t=$\frac{20}{9}$��t=$\frac{35}{12}$��
���� ������Ҫ������Բ�����ߵ����ʡ��ô���ϵ������ֱ�ߵĽ���ʽ��ֱ���ϵ������������������ȫ�ȵ��ж������ʵ�֪ʶ���ڽ������Ĺ������õ��˷������ۡ������������ϵ��������Ҫ����ѧ˼�뷽����Ӧ�������գ���Ȼ�ڣ�2��С��Ҳ��ͨ����������������Բ�İ뾶����ͨ������������ȫ�ȵõ���R���������ǽ���ڣ�3��С��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 С���Ӽҳ��������ɢ������һ�������ı�������һ�ᱨ����ɢ����һ��ʱ�䣬Ȼ��ؼң���ͼ������С����ɢ����������ҵľ���s���ף�����Һ�����ʱ��t���֣�֮��ĺ�����ϵ��������˵���д�����ǣ�������
С���Ӽҳ��������ɢ������һ�������ı�������һ�ᱨ����ɢ����һ��ʱ�䣬Ȼ��ؼң���ͼ������С����ɢ����������ҵľ���s���ף�����Һ�����ʱ��t���֣�֮��ĺ�����ϵ��������˵���д�����ǣ�������| A�� | С��������ʱ8���� | |
| B�� | С�������Զ�ľ���Ϊ400�� | |
| C�� | С���Ӽҵ������ı������е��ٶ�Ϊ50��/�� | |
| D�� | С���ӳ������ؼҹ���ʱ16���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���߶�AB�ij�Ϊ$30\sqrt{2}$����D��AB�ϣ���ACD�DZ߳�Ϊ15�ĵȱ������Σ�����D����CD��ֱ������DP����DP��һ����G������D�غϣ�������CDGH���Ǿ���CDGH�ĶԽ��߽���ΪO������OB�����߶�BO����СֵΪ��������
��ͼ���߶�AB�ij�Ϊ$30\sqrt{2}$����D��AB�ϣ���ACD�DZ߳�Ϊ15�ĵȱ������Σ�����D����CD��ֱ������DP����DP��һ����G������D�غϣ�������CDGH���Ǿ���CDGH�ĶԽ��߽���ΪO������OB�����߶�BO����СֵΪ��������| A�� | $15\sqrt{2}$ | B�� | 15 | C�� | $30\sqrt{2}$ | D�� | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
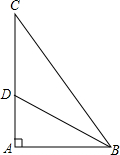 ��ͼ��ʾ����Rt��ABC�У���A=90�㣬BDƽ�֡�ABC����AC�ڵ�D����AD=2��BC=5�����BCD�������5��
��ͼ��ʾ����Rt��ABC�У���A=90�㣬BDƽ�֡�ABC����AC�ڵ�D����AD=2��BC=5�����BCD�������5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ƽ���ɼ� | ��λ�� | |
| �� | 10 | 8 | 9 | 8 | 10 | 9 | 9 | �� |
| �� | 10 | 7 | 10 | 10 | 9 | 8 | �� | 9.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=CB����ABΪֱ���ġ�O��AC�ڵ�D������C��CF��AB����CF��ȡһ��E��ʹDE=CD������AE���������н��ۣ���AD=DC���ڡ�CBA�ס�CDE����$\widehat{BD}$=$\widehat{AD}$����AEΪ��O�����ߣ�һ����ȷ�Ľ���ѡ���Ǣ٢ڢܣ�
��ͼ���ڡ�ABC�У�AB=CB����ABΪֱ���ġ�O��AC�ڵ�D������C��CF��AB����CF��ȡһ��E��ʹDE=CD������AE���������н��ۣ���AD=DC���ڡ�CBA�ס�CDE����$\widehat{BD}$=$\widehat{AD}$����AEΪ��O�����ߣ�һ����ȷ�Ľ���ѡ���Ǣ٢ڢܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У���B=30�㣬BC�Ĵ�ֱƽ���߽�AB��E������ΪD�����CE=10����ED�ij�Ϊ��������
��ͼ���ڡ�ABC�У���B=30�㣬BC�Ĵ�ֱƽ���߽�AB��E������ΪD�����CE=10����ED�ij�Ϊ��������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com