
【题目】已知在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点
(1)如图1,BE交⊙O于点F,求证:∠EFC=∠BFD;
(2)如图2,当CD也是直径,EF切⊙O于F,连接DF.若tan∠D=![]() ,求sin∠E的值.
,求sin∠E的值.

【答案】(1)见解析;(2)![]()
【解析】
(1)连接AD,BD,由圆的性质可得∠CFE=∠EDB,再证明∠ADB=∠AGD=90°,可得∠DAB=∠GDB,则∠EFC=∠BFD得证;
(2)证明△CEF∽△FED,可得EF2=CEDE,设CF=a,则DF=3a,由勾股定理可得CD=![]() ,设CE=x,则EF=3x,可求出CE=
,设CE=x,则EF=3x,可求出CE=![]() 和EF=
和EF=![]() ,可用a表示OF的长,则sin∠E的值可求出.
,可用a表示OF的长,则sin∠E的值可求出.
(1)证明:如图1,连接AD,BD,
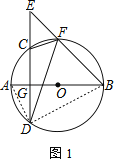
∵四边形CDBF为圆内接四边形,
∴∠CFE=∠EDB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵AB⊥CD,
∴∠AGD=90°,
∴∠GDB+∠ABD=90°,
∴∠DAB=∠GDB,
∴∠DAB=∠CFE,
∵∠DAB=∠BFD,
∴∠EFC=∠BFD;
(2)解:如图2,连接OF,CF,
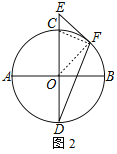
∵EF是⊙O的切线,
∴OF⊥EF,
∴∠EFO=90°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴∠EFC=∠OFD,
∵OF=OD,
∴∠ODF=∠OFD,
∴∠ODF=∠EFC,
∵∠CEF=∠FED,
∴△CEF∽△FED,
∴![]() ,
,
∴EF2=CEDE,
∵tan∠D=![]() =
=![]() ,
,
设CF=a,则DF=3a,由勾股定理可得CD=![]() ,
,
设CE=x,则EF=3x,
∴![]() ,
,
解得:x=![]() ,
,
∴![]() ,
,
∴OE=CE+OC=![]() ,
,
∴![]() =
=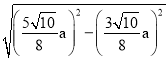 =
=![]() ,
,
∴sin∠E=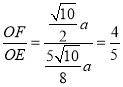 .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】张老师为了了解班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查.他将调查结果分为四类:A:很好;B:较好;C:一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)请计算出A类男生和C类女生的人数,并将条形统计图补充完整.
(2)为了共同进步,张老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
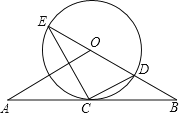
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
如图,将抛物线![]() 向右平移
向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度后,得到的抛物线
个单位长度后,得到的抛物线![]() ,平移后的抛物线
,平移后的抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .抛物线
.抛物线![]() 的对称轴
的对称轴![]() 与抛物线
与抛物线![]() 交于点
交于点![]() .
.

(1)请你直接写出抛物线![]() 的解析式;(写出顶点式即可)
的解析式;(写出顶点式即可)
(2)求出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛,故先在射击队举行了一场选拔比赛.在相同的条件下各射靶![]() 次,每次射靶的成绩情况如图所示.
次,每次射靶的成绩情况如图所示.
甲射靶成绩的条形统计图
| 乙射靶成绩的折线统计图
|
(![]() )请你根据图中的数据填写下表:
)请你根据图中的数据填写下表:
平均数 | 众数 | 方差 | |
甲 | __________ |
|
|
乙 |
| __________ | __________ |
(![]() )根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
)根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则BD的长为__________.
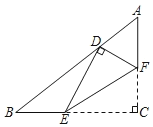
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.

(1)画出△ABC关于原点对称的△A1B1C1;
(2)画出△ABC向上平移5个单位后的△A2B2C2,并求出平移过程中△ABC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).与反比例函数的图象交于点Q,反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),则四边形PAQO的面积为( )
(O为坐标原点),则四边形PAQO的面积为( )

A.7B.10C.4+2![]() D.4﹣2
D.4﹣2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com