
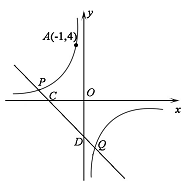
如图,反比例函数y=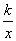 的图象经过点A(-1,4),直线y=-x + b(b≠0) 与双曲线y=
的图象经过点A(-1,4),直线y=-x + b(b≠0) 与双曲线y=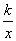 在第二、四象限分别相交于P,Q 两点,与x 轴、y 轴分别相交于C,D 两点
在第二、四象限分别相交于P,Q 两点,与x 轴、y 轴分别相交于C,D 两点
(1)求k 的值;
(2)当b=-2 时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD? 若存在,请求出b 的值;若不存在,请说明理由
科目:初中数学 来源: 题型:
在平面直角坐标系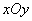 中,
中, 的半径为r,P是与圆心C不重合的点,点P关于
的半径为r,P是与圆心C不重合的点,点P关于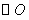 的反称点的定义如下:若
的反称点的定义如下:若 在射线CP上存在一点
在射线CP上存在一点 ,满足
,满足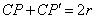 ,则称
,则称 为点P关于
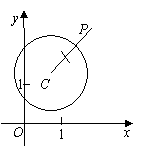
为点P关于 的反称点,下图为点P及其
的反称点,下图为点P及其 关于
关于 的反称点
的反称点 的示意图。
的示意图。
 |
(1)当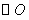 的半径为1时。
的半径为1时。
①分别判断点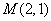 ,
,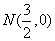 ,
,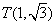 关于
关于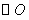 的反称点是否存在,若存
的反称点是否存在,若存 在?
在?
求其坐标;
②点P在直线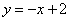 上,若点P关于
上,若点P关于 的反称点
的反称点 存在,且点
存在,且点 不在x轴上,求点P的横坐标的取值范围;
不在x轴上,求点P的横坐标的取值范围;
(2)当 的圆心在x轴上,半径为1,直线
的圆心在x轴上,半径为1,直线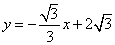 与x轴,y轴分别交于点A,B,若线段AB上存在点P,使得点P关于
与x轴,y轴分别交于点A,B,若线段AB上存在点P,使得点P关于 的反称点
的反称点 在
在 的内部,求圆心C的横坐标的取值范围。
的内部,求圆心C的横坐标的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
今年江苏省参加高考的人数约为393 000人,这个数据用科学记数法可表示为 ( )
A.393×103 B.3.93×103 C.3.93×105 D.3.93×106
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABC中,∠ACB=90º,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为 ( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.如果要求这两车间生产这批产品的总耗水量不得超过200吨,那么该厂如何分配两车间的生产任务,才能使这次生产所能获取的利润w最大?最大利润是多少?(注:利润=产品总售价-购买原材料成本-水费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com