
【题目】如图,AB是⊙O的直径,点C是BA延长线上一点,CD切⊙O于D点,弦DE∥CB,Q是AB上一动点,CA=1,CD是⊙O半径的![]() 倍.
倍.
(1)求⊙O的半径R;
(2)当Q从A向B运动的过程中,图中阴影部分的面积是否发生变化?若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积.

【答案】
【1】 ∵CD切⊙O于点D ,CD=![]() R,∴CD2=CA×CB,(
R,∴CD2=CA×CB,(![]() R)2=1×(1+2R),解得R=1,或R=-
R)2=1×(1+2R),解得R=1,或R=-![]() (舍去),∴R=1.
(舍去),∴R=1.
【2】 当点Q从点A向点B运动的过程中,图中阴影部分的面积不发生变化.
连接OD、OE, ∵DE∥CB,∴S△QDE=S△ODE(等底等高的三角形面积不变),
∴S阴影=S扇形ODE,在直角△CDO中,OD=1,CD=![]() ,CO=2,∠COD=600,
,CO=2,∠COD=600,
∴∠ODE=600,∴△ODE是等边三角形,S阴影=S扇形ODE=![]() =
=![]() .
.
【解析】
(1)根据切割线定理即可列方程求解;
(2)据弦DE∥CB,可以连接OD,OE,则阴影部分的面积就转化为扇形ODE的面积.所以阴影部分的面积不变.只需根据直角三角形的边求得角的度数即可


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】网络时代的到来,很多家庭都接入了网络,电信局规定了拨号入网两种收费方式,用户可以任选其一:A:计时制:0.05元/分;B:全月制:54元/月(限一部个人住宅电话入网).此外B种上网方式要加收通信费0.02元/分.
①某用户某月上网的时间为x小时,两种收费方式的费用分别为![]() (元)、
(元)、![]() (元),写出
(元),写出![]() 、
、![]() 与x之间的函数关系式.
与x之间的函数关系式.
②在上网时间相同的条件下,请你帮该用户选择哪种方式上网更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
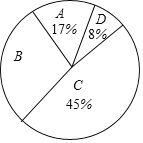
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,AB⊥AD,点E在CD的延长线上,且∠BAC=∠DAE.
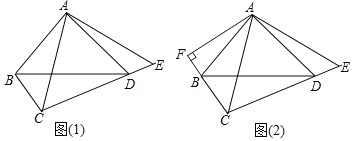
(1)求证:AC=AE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的边BC上的高,试求CE与AF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=![]() BC;④S△ACE=
BC;④S△ACE=![]() SABCD.其中正确的个数是( )
SABCD.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角ΔABC中,已知AB=AC,D为底边BC上的一点,E为线段AD上的一点,且∠BED=∠BAC=2∠DEC,连接CE.
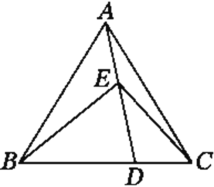
(1)求证:∠ABE=∠DAC
(2)若∠BAC=60°,试判断BD与CD有怎样的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑销售商试销某一品牌电脑(出厂为![]() 元/台)以
元/台)以![]() 元/台销售时,平均每月可销售
元/台销售时,平均每月可销售![]() 台,现为了扩大销售,销售商决定降价销售,在原来
台,现为了扩大销售,销售商决定降价销售,在原来![]() 月份平均销售量的基础上,经
月份平均销售量的基础上,经![]() 月份的市场调查,
月份的市场调查,![]() 月份调整价格后,月销售额达到
月份调整价格后,月销售额达到![]() 元.已知电脑价格每台下降
元.已知电脑价格每台下降![]() 元,月销售量将上升
元,月销售量将上升![]() 台.
台.
![]() 求
求![]() 月份到
月份到![]() 月份销售额的月平均增长率;
月份销售额的月平均增长率;
![]() 求
求![]() 月份时该电脑的销售价格.
月份时该电脑的销售价格.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com