
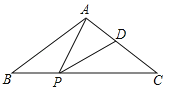
【题目】(山东泰安,第27题)(10分)如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:ACCD=CPBP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)先证∠APD=∠B=∠C,从而有△ABP∽△PCD,即可得到![]() ,即ABCD=CPBP,由AB=AC即可得到ACCD=CPBP;
,即ABCD=CPBP,由AB=AC即可得到ACCD=CPBP;
(2)由PD∥AB得到∠APD=∠BAP,进而得到∠BAP=∠C,从而有△BAP∽△BCA,根据相似三角形的性质即可求出BP的长.
试题解析:(1)∵AB=AC,∴∠B=∠C,∵∠APD=∠B,∴∠APD=∠B=∠C,∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC,∴△ABP∽△PCD,∴![]() ,∴ABCD=CPBP,∵AB=AC,∴ACCD=CPBP;
,∴ABCD=CPBP,∵AB=AC,∴ACCD=CPBP;
(2)∵PD∥AB,∴∠APD=∠BAP,∵∠APD=∠C,∴∠BAP=∠C,∵∠B=∠B,∴△BAP∽△BCA,
∴![]() .∵AB=10,BC=12,∴
.∵AB=10,BC=12,∴![]() ,∴BP=
,∴BP=![]() .
.


科目:初中数学 来源: 题型:
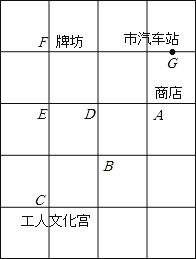
【题目】 如图是某市区四个景点或单位(A为商店,C为工人文化宫,F为牌坊,G为市汽车站)的大致平面图.可将方格的边长看作是一个单位长度.
(1)请你建立适当的直角坐标系,分别写出这四个地点的坐标.
(2)在商店A处有游客甲和游客乙,甲按线路A→D→E→F步行到达牌坊;乙按A→B→C步行到达工人文化宫,若一个单位长度代表100米,你能比较一下两人哪个走的路程较多吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并填空:
(1)为了求代数式 ![]() 的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)把一个多项式进行部分因式分解可以解决求代数式的最大(或最小)值问题.例如: ![]() =(
=( ![]() )
) ![]() =
= ![]() ,因为
,因为 ![]() 是非负数,所以,这个代数式
是非负数,所以,这个代数式 ![]() 的最小值是 , 这时相应的x的平方是.
的最小值是 , 这时相应的x的平方是.
尝试探究并解答:
(3)求代数式 ![]() 的最小值,并写出相应x的值.
的最小值,并写出相应x的值.
(4)求代数式 ![]() 的最大值,并写出相应x的值.
的最大值,并写出相应x的值.
(5)已知 ![]() ,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围).
,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com