
【题目】如图1,点![]() 为正
为正![]() 的
的![]() 边上一点(
边上一点(![]() 不与点
不与点![]() 重合),点
重合),点![]() 分别在边
分别在边![]() 上,且
上,且![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() (用含
(用含![]() 的式子表示);
的式子表示);
(3)如图2,若点![]() 为
为![]() 边的中点,求证:
边的中点,求证: ![]() .
.
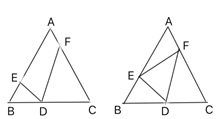
图1 图2
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)根据两角对应相等的两个三角形相似即可判断;
(2)如图2中,分别过E,F作EG⊥BC于G,FH⊥BC于H,S1=![]() BDEG=
BDEG=![]() BDEG=
BDEG=![]() aBEsin60°=
aBEsin60°=![]() aBE,S2=
aBE,S2=![]() CDFH=
CDFH=![]() bCF,可得S1S2=
bCF,可得S1S2=![]() abBECF,由(1)得△BDE∽△CFD,
abBECF,由(1)得△BDE∽△CFD,![]() ,即BEFC=BDCD=ab,即可推出S1S2=
,即BEFC=BDCD=ab,即可推出S1S2=![]() a2b2;
a2b2;
(3)想办法证明△DFE∽△CFD,推出![]() ,即DF2=EFFC;
,即DF2=EFFC;
(1)证明:如图1中,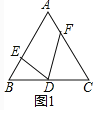
在△BDE中,∠BDE+∠DEB+∠B=180°,又∠BDE+∠EDF+∠FDC=180°,
∴∠BDE+∠DEB+∠B=∠BDE+∠EDF+∠FDC,
∵∠EDF=∠B,
∴∠DEB=∠FDC,
又∠B=∠C,
∴△BDE∽△CFD.
(2)如图2中,分别过E,F作EG⊥BC于G,FH⊥BC于H,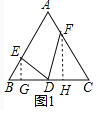
S1=![]() BDEG=
BDEG=![]() BDEG=
BDEG=![]() aBEsin60°=
aBEsin60°=![]() aBE,S2=
aBE,S2=![]() CDFH=
CDFH=![]() bCF,
bCF,
∴S1S2=![]() abBECF
abBECF
由(1)得△BDE∽△CFD,
∴![]() ,即BEFC=BDCD=ab,
,即BEFC=BDCD=ab,
∴S1S2=![]() a2b2.
a2b2.
(3)由(1)得△BDE∽△CFD,
∴![]() ,
,
又BD=CD,
∴![]() ,
,
又∠EDF=∠C=60°,
∴△DFE∽△CFD,
∴![]() ,即DF2=EFFC.
,即DF2=EFFC.


科目:初中数学 来源: 题型:
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
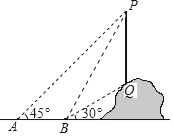
A. 6+2![]() B. 6+
B. 6+![]() C. 10﹣
C. 10﹣![]() D. 8+
D. 8+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
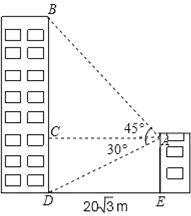
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20![]() 米.
米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
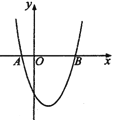
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点.若在抛物线上有且只有三个不同的点
两点.若在抛物线上有且只有三个不同的点![]() 、
、![]() 、
、![]() ,使得
,使得![]() 、
、![]() 、
、![]() 的面积都等于
的面积都等于![]() ,则
,则![]() 的值是( )
的值是( )
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
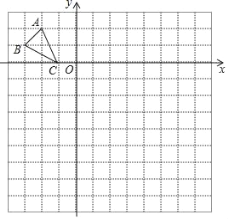
【题目】如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2,2),B(﹣3,1),C(﹣1,0).
(1)将△ABC绕点O逆时针旋转90°得到△DEF,画出△DEF;
(2)以O为位似中心,将△ABC放大为原来的2倍,在网格内画出放大后的△A1B1C1,若P(x,y)为△ABC中的任意一点,这次变换后的对应点P1的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
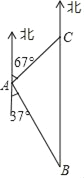
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有两条抛物线关于x轴对称,且他们的顶点相距10个单位长度,若其中一条抛物线的函数表达式为y=![]() +6x+m,则m的值是 ( )
+6x+m,则m的值是 ( )
A. -4或-14 B. -4或14 C. 4或-14 D. 4或14
查看答案和解析>>
科目:初中数学 来源: 题型:
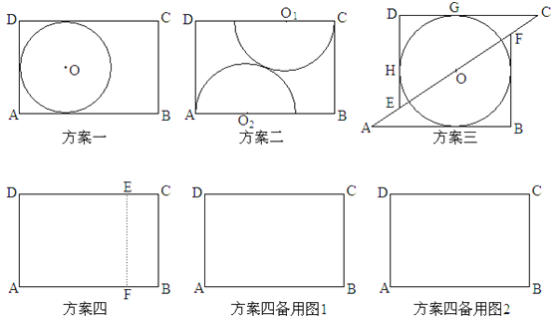
【题目】木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:
方案一:直接锯一个半径最大的圆;
方案二:圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼接到矩形AEFD下面,并利用拼成的木板锯一个尽可能大的圆。
(1)写出方案一中的圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=![]() (
(![]() ),圆的半径为
),圆的半径为![]() ,
,
①求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
②当![]() 取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?
取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com