
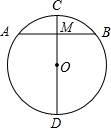
 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知AB=8,CM=2,求直径CD的长.
如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知AB=8,CM=2,求直径CD的长. 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
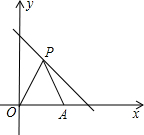 如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6的点,点A(4,0),O是坐标原点,△PAO的面积为S.
如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6的点,点A(4,0),O是坐标原点,△PAO的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )| A、AB=12m |
| B、MN∥AB |
| C、△CMN∽△CAB |
| D、CM:MA=1:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 给窗户装遮阳棚,其目的为最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,现请你为我校新建成的高中部教学楼朝南的窗户设计一个直角形遮阳蓬BCD,如图,已知窗户AB高度为h=2米,本地冬至日正午时刻太阳光与地面的最小夹角α=32°,夏至日正午时刻太阳光与地面的最大夹角β=79°,请分别计算直角形遮阳蓬BCD中BC、CD的长(结果精确到0.1米)
给窗户装遮阳棚,其目的为最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,现请你为我校新建成的高中部教学楼朝南的窗户设计一个直角形遮阳蓬BCD,如图,已知窗户AB高度为h=2米,本地冬至日正午时刻太阳光与地面的最小夹角α=32°,夏至日正午时刻太阳光与地面的最大夹角β=79°,请分别计算直角形遮阳蓬BCD中BC、CD的长(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com