
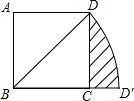
 如图,在正方形ABCD中,对角线BD的长为$\sqrt{2}$.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为弧DD′,则图中阴影部分的面积是$\frac{π}{4}-\frac{1}{2}$.
如图,在正方形ABCD中,对角线BD的长为$\sqrt{2}$.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为弧DD′,则图中阴影部分的面积是$\frac{π}{4}-\frac{1}{2}$. 分析 要求阴影部分的面积只要求出扇形BDD′和三角形BCD的面积,然后作差即可,扇形BDD′是以BD为半径,所对的圆心角是45°,根据正方形ABCD和BD的长可以求得BC的长,从而可以求得三角形BCD的面积.
解答 解:设BC的长为x,
${x}^{2}+{x}^{2}=(\sqrt{2})^{2}$
解得,x=1,
即BC=1,
∴S阴影CDD′=S扇形BDD′-S△BCD=$\frac{45×π×(\sqrt{2})^{2}}{360}-\frac{1×1}{2}$=$\frac{π}{4}-\frac{1}{2}$,
故答案为:$\frac{π}{4}-\frac{1}{2}$.
点评 本题考查扇形面积的计算、三角形的面积,解题的关键是明确题意,找出所求问题需要的条件.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
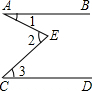 如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )
如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )| A. | ∠1+∠2=∠3 | B. | ∠1+∠2+∠3=360° | C. | ∠1+∠3=∠2 | D. | ∠1+∠2+∠3=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
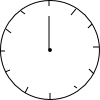 如图,一个挂钟分针长10cm,经过40分钟,它的针尖转过的弧长是( )
如图,一个挂钟分针长10cm,经过40分钟,它的针尖转过的弧长是( )| A. | 40πcm | B. | $\frac{40}{3}$πcm | C. | $\frac{20}{3}$πcm | D. | $\frac{100}{9}$πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 850×106千克 | B. | 8.50×10-4千克 | C. | 0.850×10-4千克 | D. | 850×10-4千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
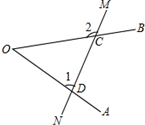 如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )
如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )| A. | 85° | B. | 75° | C. | 65° | D. | 55° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com