
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作EF⊥AB于点F,交AC的延长线于点E.
(1)判断EF与⊙O的位置关系,并说明理由;
(2)若AF=6,sinE=![]() ,求BF的长.
,求BF的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)EF与⊙O相切,先根据等腰三角形三线合一得:BD是高线也是中线,由此得OD是△ABC的中位线,所以OD∥AB,所以OD⊥EF,则EF与⊙O相切;
(2)设圆的半径为x,根据△EOD∽△EAF,列比例式求x的值,则直径AC=![]() ,则AB=
,则AB=![]() ,由此可得结论.
,由此可得结论.
解:(1)EF与⊙O相切,理由是:
连接OD、AD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∵AB=AC,
∴BD=DC,
∵OA=OC,
∴OD为△ABC的中位线,
∴OD∥AB,
∵EF⊥AB,
∴OD⊥EF,
∴EF与⊙O相切;
(2)∵OD∥AB,
∴△EOD∽△EAF,
∴![]() ,
,
Rt△AEF中,sinE=![]() =
=![]() ,
,
∵AF=6,
∴![]() =
=![]() ,
,
∴AE=10,
设OD=x,则OA=OD=x,
∴![]() ,
,
x=![]() ,
,
∴OA=![]() ,
,
∴AC=2OA=![]() ,
,
∴AB=AC=![]() ,
,
∴BF=AB﹣AF=![]() ﹣6=
﹣6=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行![]() 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九![]() 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的![]() 倍,结果比其他班提前
倍,结果比其他班提前![]() 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点A′的坐标(____________),顶点B的坐标(____________),顶点C关于原点对称的点C′的坐标(____________).
(2)△ABC的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣4ax+3a.
(Ⅰ)求该二次函数的对称轴;
(Ⅱ)若该二次函数的图象开口向下,当1≤x≤4时,y的最大值是2,且当1≤x≤4时,函数图象的最高点为点P,最低点为点Q,求△OPQ的面积;
(Ⅲ)若对于该抛物线上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合图象,直接写出t的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
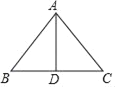
【题目】如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,将此等腰三角形纸片沿底边BC上的高AD剪成两个全等的三角形,用这两个三角形拼成一个平行四边形,则所拼出的所有平行四边形中最长的对角线的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员进行射击比赛,两人在相同条件下,各射击10次,射击的成绩如图所示.根据统计图信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | 8 | b | 8 | s2 |
乙 | a | 7 | c | 0.6 |
(1)补充表格中a,b,c的值,并求甲的方差s2;
(2)运用表中的四个统计量,简要分析这两名运动员的射击成绩,若选派其中一名参赛,你认为应选哪名运动员?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com