
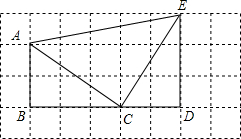
 如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.
如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由. 分析 利用勾股定理表示出AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;CE=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;AE=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$;再利用勾股定理的逆定理得到三角形为直角三角形.
解答 解:△ACE是直角三角形.理由如下:
∵在△ACE中,
AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
CE=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
AE=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$;
∴AC2+CE2=AE2,
∴∠ACE=90°,△ACE是直角三角形,
点评 本题考查了勾股定理、勾股定理逆定理、三角形的面积,充分利用网格是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周零花钱的情况 | B. | 旅客上飞机前的安检 | ||
| C. | 工厂招聘工人,对应聘人员体检 | D. | 了解全国中小学生的身高情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2或8 | B. | 2或-8 | C. | -2或8 | D. | -2或-8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com