Question

1．如图：在平面直角坐标系xOy中，已知正比例函数y=$\frac{4}{3}x$与一次函数y=-x+7的图象交于点A．
（1）求点A的坐标；
（2）在y轴上确定点M，使得△AOM是等腰三角形，请直接写出点M的坐标；
（3）如图、设x轴上一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交y=$\frac{4}{3}x$和y=-x+7的图象于点B、C，连接OC，若BC=$\frac{14}{5}$OA，求△ABC的面积及点B、点C的坐标；
（4）在（3）的条件下，设直线y=-x+7交x轴于点D，在直线BC上确定点E，使得△ADE的周长最小，请直接写出点E的坐标．

Answer 1

分析 （1）联立正比例函数与一次函数解析式组成方程组，求出方程组的解得到x与y的值，确定出A坐标即可；
（2）利用勾股定理求出OA的长，根据M在y轴上，且△AOM是等腰三角形，如图1所示，分情况讨论，求出M坐标即可；
（3）设出B与C坐标，表示出BC，由已知BC与OA关系，及OA的长求出BC的长，求出a的值，如图2所示，过A作AQ垂直于BC，求出三角形ABC面积；由a的值确定出B与C坐标即可；
（4）如图3所示，作出D关于直线BC的对应点D′，连接AD′，与直线BC交于点E，此时△ADE周长最小，求出此时E坐标即可．

解答 解：（1）联立得：$\left\{\begin{array}{l}{y=\frac{4}{3}x}\\{y=-x+7}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$，
则点A的坐标为（3，4）；
（2）根据勾股定理得：OA=$\sqrt{{3}^{2}+{4}^{2}}$=5，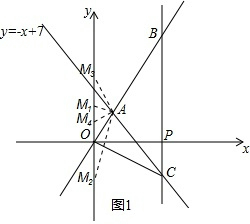

如图1所示，分四种情况考虑：
当OM₁=OA=5时，M₁（0，5）；
当OM₂=OA=5时，M₂（0，-5）；
当AM₃=OA=5时，M₃（0，8）；
当OM₄=AM₄时，M₄（0，$\frac{25}{8}$），
综上，点M为（0，5）、（0，-5）、（0，8）、（0，$\frac{25}{8}$）；
（3）设点B（a，$\frac{4}{3}$a），C（a，-a+7），
∵BC=$\frac{14}{5}$OA=$\frac{14}{5}$×5=14，
∴$\frac{4}{3}$a-（-a+7）=14，
解得：a=9，
过点A作AQ⊥BC，如图2所示，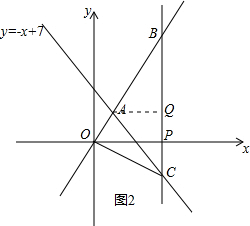

∴S_△ABC=$\frac{1}{2}$BC•AQ=$\frac{1}{2}$×14×（9-3）=42，
当a=9时，$\frac{4}{3}$a=$\frac{4}{3}$×9=12，-a+7=-9+7=-2，
∴点B（9，12）、C（9，-2）；
（4）如图3所示，作出D关于直线BC的对称点D′，连接AD′，与直线BC交于点E，连接DE，此时△ADE周长最小，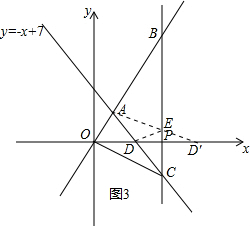

对于直线y=-x+7，令y=0，得到x=7，即D（7，0），
由（3）得到直线BC为直线x=9，
∴D′（11，0），
设直线AD′解析式为y=kx+b，
把A与D′坐标代入得：$\left\{\begin{array}{l}{3k+b=4}\\{11k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{11}{2}}\end{array}\right.$，
∴直线AD′解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$，
令x=9，得到y=1，
则此时点E坐标为（9，1）．

点评 此题属于一次函数综合题，涉及的知识有：两直线的交点，坐标与图形性质，待定系数法确定一次函数解析式，对称的性质，等腰三角形的性质，勾股定理，坐标与图形性质，熟练掌握一次函数的性质是解本题的关键．