
【题目】某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人、2人、3人、4人、5人分别记为A、B、C、D、E,由调查所得数据绘制了如图所示的不完整的统计图表.
类别 | 频率 |
A | m |
B | 0.35 |
C | 0.20 |
D | n |
E | 0.05 |
(1)求本次调查的小型汽车数量及m,n的值;
(2)补全频数分布直方图;

(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中每车只乘坐1人的小型汽车数量.
【答案】(1)本次调查的小型汽车数量为160辆,m=0.3,n=0.1;(2)见解析;(3)估计其中每车只乘坐1人的小型汽车数量为1500辆.
【解析】
(1)由C类别数量及其对应的频率可得总数量,再由频率=频数÷总数量可得m、n的值;
(2)用总数量乘以B、D对应的频率求得其人数,从而补全图形;
(3)利用样本估计总体思想求解可得.
(1)本次调查的小型汽车数量为32÷0.2=160(辆),
m=48÷160=0.3,n=1﹣(0.3+0.35+0.20+0.05)=0.1;
(2)B类小汽车的数量为160×0.35=56,D类小汽车的数量为0.1×160=16,
补全图形如下:
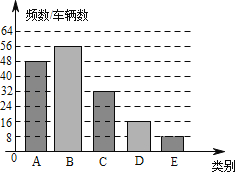
(3)估计其中每车只乘坐1人的小型汽车数量为5000×0.3=1500(辆).


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
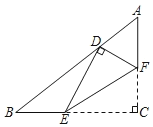
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则BD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=a(x-1)2+k与x轴两个交点间的距离为2,将抛物线y=a(x-1)2+k向上平移n个单位,平移后的抛物线经过点(m,n),则m的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).与反比例函数的图象交于点Q,反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),则四边形PAQO的面积为( )
(O为坐标原点),则四边形PAQO的面积为( )

A.7B.10C.4+2![]() D.4﹣2
D.4﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.

(1)当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.
(2)如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:
①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.
(参考数据:![]() ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )

A. 小球的飞行高度不能达到15m
B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s
D. 小球飞出1s时的飞行高度为10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com