
分析 (1)先将式子中的二次根式化简,绝对值符号去掉,然后再合并同类项即可解答本题;
(2)先把括号内的式子能化简的先化简,把除法转化为乘法,然后再根据乘法分配律进行计算即可.
解答 解:(1)$\sqrt{12}+\left|{2-\sqrt{3}}\right|+{(\sqrt{3})^2}$
=$2\sqrt{3}+2-\sqrt{3}+3$
=$\sqrt{3}+5$;
(2)($\frac{3}{4}$$\sqrt{15}$-$\sqrt{12}$)÷$\frac{\sqrt{3}}{2}$
=$(\frac{3\sqrt{15}}{4}-2\sqrt{3})×\frac{2}{\sqrt{3}}$
=$\frac{3\sqrt{15}}{4}×\frac{2}{\sqrt{3}}-2\sqrt{3}×\frac{2}{\sqrt{3}}$
=$\frac{3\sqrt{5}}{2}-4$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
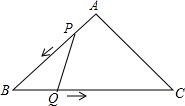 已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:
已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a<\frac{3}{2}$ | B. | $a≤\frac{3}{2}$ | C. | $a>\frac{3}{2}$ | D. | $a≥\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
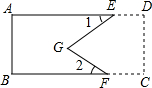 有一块长方形钢板ABCD,现将它加工成如图所示的零件,按规定∠1、∠2应分别为45°和30°.检验人员量得∠EGF为78°,就判断这个零件不合格,你能说明理由吗?
有一块长方形钢板ABCD,现将它加工成如图所示的零件,按规定∠1、∠2应分别为45°和30°.检验人员量得∠EGF为78°,就判断这个零件不合格,你能说明理由吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com