Question

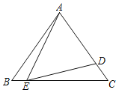
【题目】如图所示，在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，试说明AD与EF的位置关系.

Answer 1

【答案】AD⊥EF，且AD平分EF，理由见解析.

【解析】

根据角平分线的性质得到∠EAD=∠FAD，DE=DF，易证△AED≌△AFD，从而得到AE=AF，然后可证△AEG≌△AFG，得到EG=FG，∠AGE=∠AGF=90°，从而得出结论.

解：AD⊥EF，且AD平分EF，理由如下：

∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F

∴∠EAD=∠FAD，DE=DF，∠AED=∠AFD=90°，

在△AED和△AFD中，

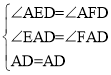
∴△AED≌△AFD（AAS）

∴AE=AF

在△AEG和△AFG中，

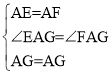
∴△AEG≌△AFG（SAS）

∴EG=FG，∠AGE=∠AGF=90°

即AD⊥EF，且AD平分EF.