
| 2 |
| 3 |
| 3 |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
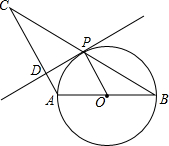 如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点P,PD⊥AC于点D
如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点P,PD⊥AC于点D查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
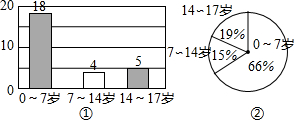 小明、小亮和小丽想要了解他们所生活的小区里小朋友的年龄情况,小明调查了当天在院子里玩耍的小朋友,调查情况如图①所示;小亮调查了他所居住的二单元的小朋友,情况如图②所示;小丽调查了每个单元一楼的两家住户中小朋友的年龄,数据如下(单位:岁):3、16、14、15、17、8、4、6、9、7、17、12、2、13、6、5、12、14、3、15、5、16、1、1.
小明、小亮和小丽想要了解他们所生活的小区里小朋友的年龄情况,小明调查了当天在院子里玩耍的小朋友,调查情况如图①所示;小亮调查了他所居住的二单元的小朋友,情况如图②所示;小丽调查了每个单元一楼的两家住户中小朋友的年龄,数据如下(单位:岁):3、16、14、15、17、8、4、6、9、7、17、12、2、13、6、5、12、14、3、15、5、16、1、1.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com