
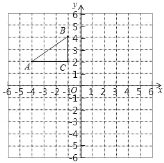
【题目】在平面直角坐标系中,Rt△ABC 的三个顶点分别是 A(﹣4,2),B(﹣1,4),C(﹣1,2).
(1)将△ABC 以点 C 为旋转中心旋转 180°,画出旋转后对应的△![]() ,
,![]() 的坐标为 ;
的坐标为 ;
(2)平移△ABC,点 B 的对应点 ![]() 的坐标为(4,﹣1),画出平移后对应的△
的坐标为(4,﹣1),画出平移后对应的△![]() ,
,![]() 的坐标为 ;
的坐标为 ;
(3)若将△![]() 绕某一点旋转可以得到△
绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标 为 .
,请直接写出旋转中心的坐标 为 .
科目:初中数学 来源: 题型:
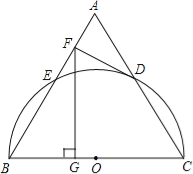
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
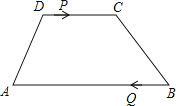
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展“环境治理留住青山绿水,绿色发展赢得金山银山”活动,对其周边的环境污染进行综合治理.![]() 年对
年对![]() 、
、![]() 两区的空气量进行监测,将当月每天的空气污染指数(简称:
两区的空气量进行监测,将当月每天的空气污染指数(简称:![]() )的平均值作为每个月的空气污染指数,并将
)的平均值作为每个月的空气污染指数,并将![]() 年空气污染指数绘制如下表.据了解,空气污染指数
年空气污染指数绘制如下表.据了解,空气污染指数![]() 时,空气质量为优:
时,空气质量为优:![]() 空气污染指数
空气污染指数![]() 时,空气质量为良:
时,空气质量为良:![]() 空气污染指数
空气污染指数![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
月份 地区 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请求出![]() 、
、![]() 两区的空气污染指数的平均数;
两区的空气污染指数的平均数;
(2)请从平均数、众数、中位数、方差等统计量中选两个对![]() 区、
区、![]() 区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
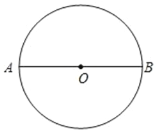
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
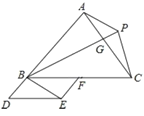
【题目】如图,点![]() 是
是![]() 的边
的边![]() 的延长线上一点,点
的延长线上一点,点![]() 是边
是边![]() 上的一点(不与点
上的一点(不与点![]() 重合).以
重合).以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,又
,又![]() (点
(点![]() 、
、![]() 在直线
在直线![]() 的同侧),如果
的同侧),如果![]() ,那么
,那么![]() 的面积与
的面积与![]() 面积的比值为____________.
面积的比值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() 的三个顶点在坐标轴上,
的三个顶点在坐标轴上,![]() ,且
,且![]() ,将
,将![]() 沿着
沿着![]() 翻折到
翻折到![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以
轴以![]() 个单位秒的速度向终点
个单位秒的速度向终点![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,分别交直线
轴,分别交直线![]() 、直线
、直线![]() 于点
于点![]() 、
、![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 运动时间为
运动时间为![]() 秒,求
秒,求![]() 与
与![]() 的关系式,并写出
的关系式,并写出![]() 的取值范围.
的取值范围.
(3如图2在(2)的条件下,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 值和点
值和点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
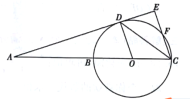
【题目】如图,点D是⊙O上一点,直线AE经过点D,直线AB经过圆心O,交⊙O于B,C两点,CE⊥AE,垂足为点E,交⊙O于点F,∠BCD=∠DCF
(1)求∠A+∠BOD的度数;
(2)若sin∠DCE=![]() ,⊙O的半径为5,求线段AB的长.
,⊙O的半径为5,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
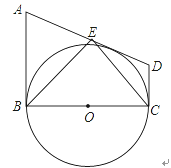
【题目】如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
(1)AB+CD=AD;(2)S△BCE=S△ABE+S△DCE;(3)ABCD=![]() ;(4)∠ABE=∠DCE.
;(4)∠ABE=∠DCE.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com