
【题目】旅行社组团去外地考察学习,10人起组团,每人单价1200元.该旅行社对超过10人的团给予优惠,即考察团每增加一人,每人的单价就降低20元.(每人单价不能低于800元)当考察团人数为多少人时,该旅行社可以获得最大营业额?最大营业额是多少?
【答案】当考察团人数为35人时,该旅行社可以获得最大营业额,最大营业额是24500元.
【解析】
当0≤x≤10时,每人单价为1200元;当x>0时,根据每人单价=原定每人单价﹣因人数增减而减少的价格,可列函数关系;根据营业额=每人单价×人数,分别列出0≤x≤10、x>10的函数关系式,求出相应范围内的最值,比较可得.
解:当0≤x≤10时,y=1200;
当10<x≤30时,y=1200﹣20(x﹣10)=﹣20x+1400;
故y与x间的函数关系式为:y=![]() ,
,
设旅行社可以获的营业额为W元,
当0≤x≤10时,W=1200x;
∵W随x的增大而增大,
∴当x=10时,W取得最大值,最大值为12000元;
W=(﹣20x+1400)x=﹣20x2+1400x=﹣20(x﹣35)2+24500,
∴当x=35时,W取得最大值,最大值为W=24500元,
综上,当x=35时,W取得最大值24500元.
答:当考察团人数为35人时,该旅行社可以获得最大营业额,最大营业额是24500元.


科目:初中数学 来源: 题型:
【题目】小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了一个不透明的袋子中装有1个红球和2个白球,这些球除颜色外都相同,随机摸出一个球后,放回并搅匀,再随机摸出一个球,如果两次摸到的球颜色相同,则小敏去;如果两次摸到的球颜色不同,则哥哥去.这个游戏规则公平吗?请说明理由; (请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
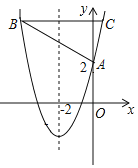
【题目】如图,抛物线y=x2+bx+c与y轴交于点A(0,2),对称轴为直线x=﹣2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)求此抛物线的解析式.
(2)点P在x轴上,直线CP将△ABC面积分成2:3两部分,请直接写出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,![]() 是直角三角形
是直角三角形![]() ,
,![]() ,
,![]() ,点
,点![]() 由点
由点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 由点
由点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,若
的速度运动,若![]() 、
、![]() 同时开始运动。
同时开始运动。
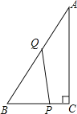
(1)运动多少秒时![]() 是直角三角形?
是直角三角形?
(2)运动多少秒时△![]() 的面积是
的面积是![]() 面积的
面积的![]() ?
?
(3)运动多少秒时![]() 的长度是
的长度是![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
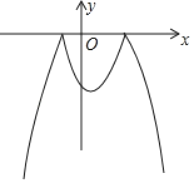
【题目】已知二次函数y=﹣x2+x+6及一次函数y=x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=x+m与这个新图象有四个交点时,m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
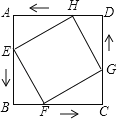
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,运动时间t=_____秒时四边形EFGH的面积最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
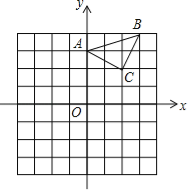
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)作出△ABC关于原点O成中心对称的△A3B3C3,并直接写出B3的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com