
【题目】如图,已知ABCD是边长为3的正方形,点P在线段BC上,点G在线段AD上,PD=PG,DF⊥PG于点H,交AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.
(1)求证:DF=PG;
(2)若PC=1,求四边形PEFD的面积.
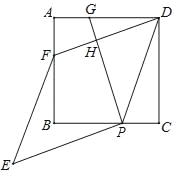
【答案】(1)证明见解析;(2)8.
【解析】
作PM⊥AD,在四边形ABCD和四边形ABPM证AD=PM;DF⊥PG,得出∠GDH+∠DGH=90°,推出∠ADF=∠MPG;还有两个直角即可证明△ADF≌△MPG,从而得出对应边相等
(2)由已知得,DG=2PC=2;△ADF≌△MPG得出DF=PD;根据旋转,得出∠EPG=90°,PE=PG从而得出四边形PEFD为平行四边形;根据勾股定理和等量代换求出边长DF的值;根据相似三角形得出对应边成比例求出GH的值,从而求出高PH 的值;最后根据面积公式得出
解:(1)证明:∵四边形ABCD为正方形,
∴AD=AB,
∵四边形ABPM为矩形,
∴AB=PM,
∴AD=PM,
∵DF⊥PG,
∴∠DHG=90°,
∴∠GDH+∠DGH=90°,
∵∠MGP+∠MPG=90°,
∴∠GDH=∠MPG,
在△ADF和△MPG中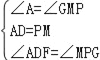 ,
,
∴△ADF≌△MPG(ASA),
∴DF=PG;
(2)作PM⊥DG于M,如图,
∵PD=PG,
∴MG=MD,
∵四边形ABCD为矩形,
∴PCDM为矩形,
∴PC=MD,
∴DG=2PC=2;
∵△ADF≌△MPG(ASA),
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF,
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
在Rt△PCD中,PC=1,CD=3,
∴PD=![]() =
=![]() ,
,
∴DF=PG=PD=![]() ,
,
∵四边形CDMP是矩形,
∴PM=CD=3,MD=PC=1,
∵PD=PG,PM⊥AD,
∴MG=MD=1,DG=2,
∵∠GDH=∠MPG,∠DHG=∠PMG=90°,
∴△DHG∽△PMG,
∴![]() ,
,
∴GH=![]() =
=![]() ,
,
∴PH=PG﹣GH=![]() ﹣
﹣![]() =
=![]() ,
,
∴四边形PEFD的面积=DFPH=![]() ×
×![]() =8.
=8.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
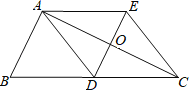
【题目】如图,已知△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
(1)求证:四边形ADCE是平行四边形;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸到球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近______;(精确到0.1);
很大时,摸到白球的频率将会接近______;(精确到0.1);
(2)假如随机摸一次,摸到白球的概率P(白球)=______;
(3)试估算盒子里白色的球有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )

A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
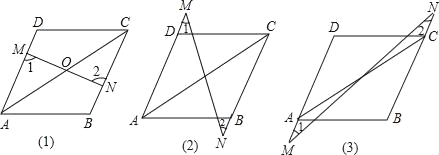
【题目】如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由;
若过O点的直线旋转至图(2)、(3)的情况,其余条件不变,那么图(1)中的∠1与∠2的关系成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )
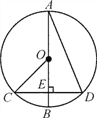
A. ∠BOC=2∠BAD B. CE=EO C. ∠OCE=40° D. AD=2OB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com