
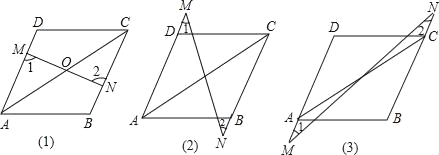
【题目】如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由;
若过O点的直线旋转至图(2)、(3)的情况,其余条件不变,那么图(1)中的∠1与∠2的关系成立吗?请说明理由.
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示.其中说法正确的是( )
(分钟)之间的函数关系如图所示.其中说法正确的是( )
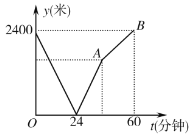
A.甲的速度是60米/分钟B.乙的速度是80米/分钟
C.点![]() 的坐标为
的坐标为![]() D.线段
D.线段![]() 所表示的函数表达式为
所表示的函数表达式为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
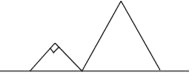
【题目】如图,直角边长为![]() 的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
A. 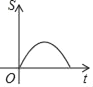 B.
B. 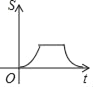
C. 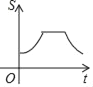 D.
D. 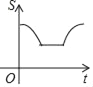
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD是边长为3的正方形,点P在线段BC上,点G在线段AD上,PD=PG,DF⊥PG于点H,交AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.
(1)求证:DF=PG;
(2)若PC=1,求四边形PEFD的面积.
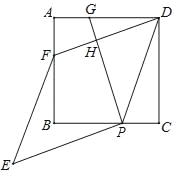
查看答案和解析>>
科目:初中数学 来源: 题型:
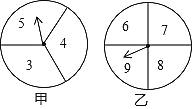
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后, 若指针所指区域内两数和等于 12,则李燕获胜;若指针所指区域内两数和等于 13,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
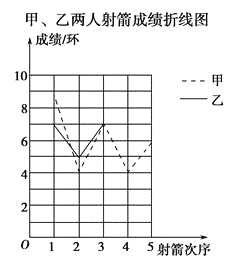
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
小宇的作业:
解:![]() 甲=
甲=![]() (9+4+7+4+6)=6,
(9+4+7+4+6)=6,
s甲2=![]() [(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]
[(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]
=![]() (9+4+1+4+0)
(9+4+1+4+0)
=3.6
小宇的作业:
解:![]() 甲=
甲=![]() (9+4+7+4+6)=6,
(9+4+7+4+6)=6,
s甲2=![]() [(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]
[(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]
=![]() (9+4+1+4+0)
(9+4+1+4+0)
=3.6
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a=________,![]() 乙=________;
乙=________;
(2)请完成图中表示乙成绩变化情况的折线;
(3)①观察图,可看出________的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
②请你从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
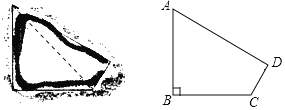
【题目】在海洋上有一近似于四边形的岛屿,其平面如图甲,小明据此构造处该岛的一个数学模型(如图乙四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5千米,CD=![]() 干米,AD=4
干米,AD=4![]() 干米.
干米.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com