
分析 (1)观察上面几个式子,发现:左边两个因数的十位数字相同,个位数字和是10;则右边的结果是一个四位数,其中个位和十位上的数是左边两个因数的个位相乘,百位和千位上的数是左边十位上的数字和大于十位数字1的数相乘.根据这一规律即可写出81×89=7209;
(2)归纳总结得到的规律用n,a及b表示出来,左右两边化简后可得出左右两边相等,得证.
解答 解:(1)∵16×14=224=1×(1+1)×100+6×4;
23×27=621=2×(2+1)×100+3×7;
32×38=1216=3×(3+1)×100+2×8;
…,
∴81×89=8×(8+1)×100+1×9=7209;
(2)发现的规律为:(10n+a)•(10n+b)=100n(n+1)+ab,
∵a+b=10,
∴等式左边=100n2+10bn+10an+ab=100n2+10n(a+b)+ab=100n2+100n+ab,
右边=100n2+100n+ab,
∴左边=右边,
则(10n+a)•(10n+b)=100n(n+1)+ab.
点评 此题主要考查了整式混合运算的应用,找出题中的规律是解本题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:选择题
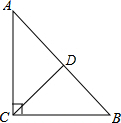 如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $±\sqrt{5}$ | D. | ±2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com