
已知抛物线抛物线y n=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
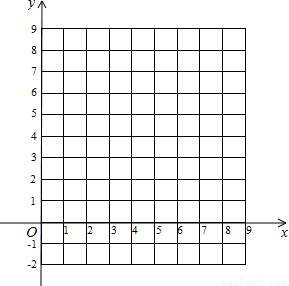
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
(1)a1=1,b1=2,y2=-(x-4)2+4.(2)y3的顶点坐标为(9,9).yn的顶点坐标为(n2,n2).y=x.(3)A0A1=2.An-1An=2n.
【解析】
试题分析:(1)因为点A0(0,0)在抛物线y1=-(x-a1)2+a1上,可求得a1=1,则y1=-(x-1)2+1;令y1=0,求得A1(2,0),b1=2;再由点A1(2,0)在抛物线y2=-(x-a2)2+a2上,求得a2=4,y2=-(x-4)2+4.
(2)求得y1的顶点坐标(1,1),y2的顶点坐标(4,4),y3的顶点坐标(9,9),依此类推,yn的顶点坐标为(n2,n2).因为所有抛物线顶点的横坐标等于纵坐标,所以顶点坐标满足的函数关系式是:y=x.
(3)①由A0(0,0),A1(2,0),求得A0A1=2;yn=-(x-n2)2+n2,令yn=0,求得An-1(n2-n,0),An(n2+n,0),所以An-1An=(n2+n)-(n2-n)=2n;
②设直线解析式为:y=kx-2k,设直线y=kx-2k与抛物线yn=-(x-n2)2+n2交于E(x1,y1),F(x2,y2)两点,联立两式得一元二次方程,得到x1+x2=2n2-k,x1•x2=n4-n2-2k.然后作辅助线,构造直角三角形,求出EF2的表述式为:EF2=(k2+1)[4n2•(1-k)+k2+8k],可见当k=1时,EF2=18为定值.所以满足条件的直线为:y=x-2.
试题解析:(1)∵当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0),
∴0=-(0-a1)2+a1,解得a1=1或a1=0.
由已知a1>0,∴a1=1,
∴y1=-(x-1)2+1.
令y1=0,即-(x-1)2+1=0,解得x=0或x=2,
∴A1(2,0),b1=2.
由题意,当n=2时,第2条抛物线y2=-(x-a2)2+a2经过点A1(2,0),
∴0=-(2-a2)2+a2,解得a2=1或a2=4,
∵a1=1,且已知a2>a1,
∴a2=4,
∴y2=-(x-4)2+4.
∴a1=1,b1=2,y2=-(x-4)2+4.
(2)抛物线y2=-(x-4)2+4,令y2=0,即-(x-4)2+4=0,解得x=2或x=6.
∵A1(2,0),
∴A2(6,0).
由题意,当n=3时,第3条抛物线y3=-(x-a3)2+a3经过点A2(6,0),
∴0=-(6-a3)2+a3,解得a3=4或a3=9.
∵a2=4,且已知a3>a2,
∴a3=9,
∴y3=-(x-9)2+9.
∴y3的顶点坐标为(9,9).
由y1的顶点坐标(1,1),y2的顶点坐标(4,4),y3的顶点坐标(9,9),
依此类推,yn的顶点坐标为(n2,n2).
∵所有抛物线顶点的横坐标等于纵坐标,
∴顶点坐标满足的函数关系式是:y=x.
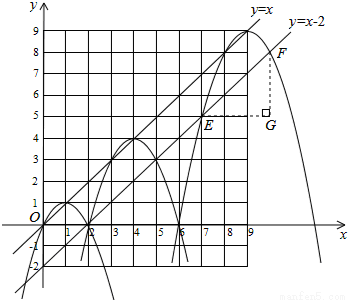
(3)∵A0(0,0),A1(2,0),
∴A0A1=2.
yn=-(x-n2)2+n2,令yn=0,即-(x-n2)2+n2=0,
解得x=n2+n或x=n2-n,
∴An-1(n2-n,0),An(n2+n,0),即An-1An=(n2+n)-(n2-n)=2n.
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年江苏省八年级12月月考数学试卷(解析版) 题型:填空题
函数y=-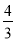 x+4的图像与x轴和y轴的交点分别为A、B,P为直线AB上的一个动点,则OP的最小值是_________.
x+4的图像与x轴和y轴的交点分别为A、B,P为直线AB上的一个动点,则OP的最小值是_________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在平行四边形ABCD中,E为AB的中点,G是对角线AC上一点,且AG:GC=1:5,EG的延长线交AD于点F,则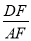 的值为( )
的值为( )

A.2 B.2.5 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
若一个三角形两边的长分别是3和7,且第三边的长恰好是方程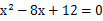 的一个实数根,则这个三角形的周长为( )
的一个实数根,则这个三角形的周长为( )
A.12 B.15 C.16 D.12或15
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:解答题
某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:填空题
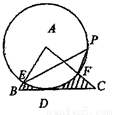
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是__________(结果保留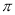 )
)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:解答题
为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.
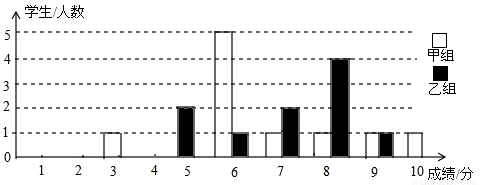
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省咸宁市中考模拟考试数学试卷(解析版) 题型:选择题
某班团支部统计了该班甲、乙、丙、丁四名同学在5月份“书香校园”活动中的课外阅读时间,他们平均每天课外阅读时间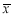 与方差s2如表所示,你认为表现最好的是( ).
与方差s2如表所示,你认为表现最好的是( ).
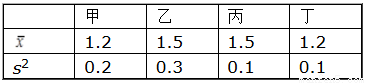
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com