
为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.
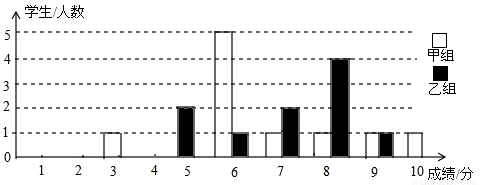
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组同学观点的理由.
(1)6;7.1;(2)甲;(3)乙.
【解析】
试题分析:(1)将甲组成绩按照从小到大的顺序排列,找出第5、6个成绩,求出平均数即为甲组的中位数;找出乙组成绩,求出乙组的平均分,填表即可;
(2)观察表格,成绩为7分处于中游略偏上,应为甲组的学生;
(3)乙组的平均分高于甲组,中位数高于甲组,方差小于甲组,所以乙组成绩好于甲组.
试题解析:(1)甲组的成绩为:3,6,6,6,6,6,7,8,9,10,甲组中位数为6,乙组成绩为5,5,6,7,7,8,8,8,8,9,平均分为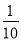 (5+5+6+7+7+8+8+8+8+9)=7.1(分),
(5+5+6+7+7+8+8+8+8+9)=7.1(分),
填表如下:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 6 | 3.41 | 90% | 20% |
乙组 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(2)观察上表可知,小明是甲组的学生;
(3)①乙组同学平均分高于甲组;②乙组同学的方差小,比甲组稳定,而且集中在中上游,所以支持乙能同学的观点.
考点:1.条形统计图;2.加权平均数;3.中位数;4.方差.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年北京市八年级上学期期中检测数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC= °.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:解答题
已知抛物线抛物线y n=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:解答题
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
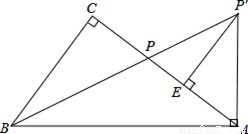
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当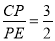 ,,BP′=5
,,BP′=5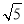 时,求线段AB的长.
时,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:填空题
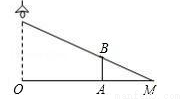
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:选择题
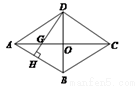
如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=( ).
A.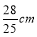 B.
B.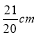 C.
C.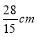 D.
D.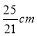
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省咸宁市中考模拟考试数学试卷(解析版) 题型:填空题
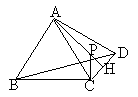
如图,AB=BC=CA=AD=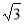 , AH⊥CD于H,CP⊥BC交AH于点P,AP=
, AH⊥CD于H,CP⊥BC交AH于点P,AP=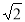 ,则BD=______.
,则BD=______.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都十校八年级12月联谊月考数学试卷(解析版) 题型:解答题
(本题12分)已知:如图1,点D是边长为2的等边△ABC边BC所在直线上的一动点,从点B向C方向运动,以AD为边向右侧作等边△ADE。
(1)连接CE,若点D在边BC上时,易知线段CE 、CD、AC三者之间的关系为CE+CD=AC; 如图2当点D在C的右侧时,试探索线段CE 、CD、AC三者之间的数量关系,并说明理由。
(2如图1,当点D从B运动到C时,①直接写出△CDE周长的最小值。②直接写出点E的运动路径长。
(3)若将题目中条件“等边△ADE”改为“满足∠ADE=60°与等边△ABC的外角平分线交于点E”,那么CE与BD还相等吗?如图3请作出判断并给出说明。



图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com