
如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
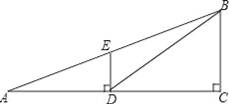

【考点】解直角三角形的应用-仰角俯角问题.
【专题】应用题.
【分析】由ED与BC都和AC垂直,得到ED与BC平行,得到三角形AED与三角形ABC相似,由相似得比例,在直角三角形AED中,利用锐角三角函数定义求出AD的长,在直角三角形BDC中,利用锐角三角函数定义求出BC的长即可.
【解答】解:∵ED⊥AC,BC⊥AC,
∴ED∥BC,
∴△AED∽△ABC,
∴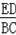
 =
=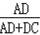
 ,
,
在Rt△AED中,DE=12米,∠A=22°,
∴tan22°=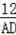
 ,即AD=
,即AD=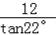
 =30米,
=30米,
在Rt△BDC中,tan∠BDC=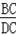
 ,即tan38.5°=
,即tan38.5°=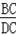
 =0.8①,
=0.8①,
∵tan22°=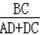
 =
=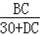
 =0.4②,
=0.4②,
联立①②得:BC=24米.
【点评】此题考查了解直角三角形的应用﹣仰角俯角问题,涉及的知识有:相似三角形的判定与性质,锐角三角函数定义,熟练掌握锐角三角函数定义是解本题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是x=2,与x轴的一个交点是(﹣1,0),有下列结论:
①abc>0;
②4a﹣2b+c<0;
③4a+b=0;
④抛物线与x轴的另一个交点是(5,0);
⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1=y2.
其中正确的是( )
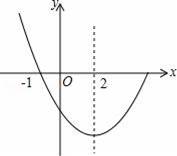

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com