
如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)
(1)求抛物线的解析式;
(2)点M为抛物线上一点,恰使△MOA≌△MOB,求点M的坐标;
(3)y轴上是否存在一点N,恰好使得△PNB为直角三角形?若存在,直接写出满足条件的所有点M的坐标;若不存在,请说明理由.


【考点】二次函数综合题.
【分析】(1)由正方形的性质可知OA=OB=3,从而得到点A的坐标,设抛物线的解析式为y=a(x﹣1)2+4,把A(0,3)代入可求得a的值,从而得到抛物线的解析式;
(2)由全等三角形对应边相等可知MA=BM,从而可知点M在AB的垂直平分线上,故此点M为直线OC与抛物线的交点,然后求得直线OC与抛物线的交点坐标即可;
(3)设N(0,t).分为∠PNB=90、∠NPB=90°、∠PBN=90°三种情况画出图形,然后依据相似三角形对应边成比例列出关于t的方程求解即可.
【解答】解:(1)∵正方形的边长为3,
∴A(0,3),B(3,0).
设抛物线的解析式为y=a(x﹣1)2+4.
∵把A(0,3)代入得:a+4=3,解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3.
(2)如图1所示:
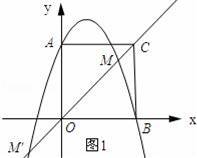

∵△MOA≌△MOB,
∴AM=BM.
∴点M在AB的垂直平分线上.
∵OACB为正方形,
∴OC为AB的垂直平分线.
设OC的解析式为y=kx,
∵将C(3,3)代入得:3k=3,解得:k=1,
∴直线OC的解析式为y=x.
由y=x与y=﹣x2+2x+3得:x=﹣x2+2x+3,解得:x1=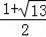
 ,x2=
,x2=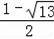
 .
.
∴M(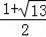
 ,
,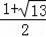
 ),M′(
),M′(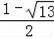
 ,
,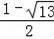
 ).
).
∴点M的坐标为(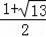
 ,
,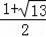
 )或(
)或(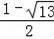
 ,
,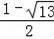
 ).
).
(3)设N(0,t).
①当∠PNB=90时,如图2所示.连接PN、BN,过点P作PM⊥y轴,垂足为M.
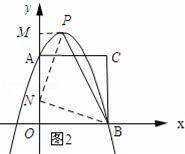

由△PMN∽△NOB,得: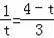
 ,解得:t1=1,t2=3.
,解得:t1=1,t2=3.
②当∠NPB=90°时.
如图3所示;连接PN、BN,过点P作x轴的平行线,交BC延长线与点M.
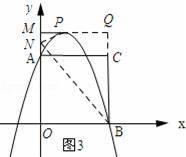

由△PMN∽△NOB,得:
 ,解得:t=
,解得:t=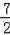
 .
.
③当∠PBN=90°时,如图4所示,过点P作x轴的平行线,交BC延长线与点M.
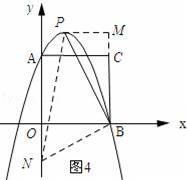

由△PMB∽△NOB得: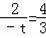
 ,解得:t=﹣
,解得:t=﹣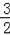
 .
.
综上所述,点M的坐标为(0,1)、(0,3)、(0,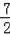
 )、(0,﹣
)、(0,﹣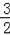
 ).
).
【点评】本题主要考查的是二次函数的综合应用,解答本题需要熟练掌握待定系数法求函数解析式的步骤和方法、二次函数表达式的三种基本形式、相似三角形的性质、正方形的性质,分类讨论是解题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
某课外活动小组为了了解本校学生上网目的,随机调查了本校的部分学生,根据调查结果,统计整理并制作了如下尚不完整的统计图:根据以上信息解答下列问题:

(1)参与本次调查的学生共有 人;
(2)在扇形统计图中,m的值为 ;
(3)补全条形统计图;
(4)中学生上网玩游戏、聊天交友已经对正常的学习产生较多负面影响,为此学校计划开展一次“合理上网”专题讲座,每班随机抽取15名学生参加,小明所在的班级有50名学生,他被抽到听讲座的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com