
����Ŀ����ͼ��
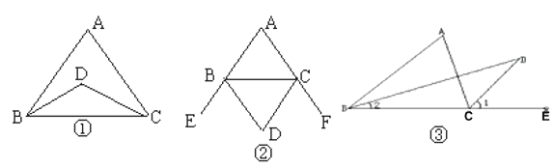
��1����ͼ����BD��CD����ABC����ACB�Ľ�ƽ�������ཻ�ڵ�D������A =70�㣬������BDC�Ķ�������˵�����ɡ�
��2����ͼ����BD��CD�ֱ��ǡ�ABC�����EBC����FCB��ƽ�������ཻ�ڵ�D������A =x�㣬����x��ʾ��BDC�Ķ�������˵�����ɡ�
��3����ͼ�ۣ�BD��CD�ֱ�����ABC�͡�ACB��ǡ�ACE��ƽ�������ཻ�ڵ�D�����ҳ���A����BDC֮���������ϵ����˵�����ɡ�
���𰸡���1����BDC��125�������ɼ���������2����BDC��90��![]() x�������ɼ���������3����BDC��
x�������ɼ���������3����BDC��![]() ��A�����ɼ�����.
��A�����ɼ�����.
��������
��1���ȸ����������ڽǺͶ��������ABC����ACB��110�����ٸ��ݽ�ƽ���ߵ����ʺ��������ڽǺͶ�����⼴�ɣ�
��2���ȸ������ƽ���ߵ����������CBD��![]() ����A����ACB������BCD��
����A����ACB������BCD��![]() ����A����ABC���������������ڽǺͶ�����ɣ�
����A����ABC���������������ڽǺͶ�����ɣ�
��3�����������ε�һ����ǵ������������ڵ������ڽǵĺͿɵá�ACE����A����ABC����DCE����D����DBC���ٸ��ݽ�ƽ���ߵĶ���ɵá�DBC��![]() ��ABC����DCE��
��ABC����DCE��![]() ��ACE��Ȼ�������ɵá�BDC��
��ACE��Ȼ�������ɵá�BDC��![]() ��A.
��A.
�⣺��1����BDC��125����
���ɣ���BD��CD�ǡ�ABC�͡�ACB�Ľ�ƽ���ߣ�
���DBC��![]() ��ABC����DCB��
��ABC����DCB��![]() ��ACB��
��ACB��
�ߡ�ABC����ACB��180����A��110����
���BDC��180����DBC��DCB��180��![]() ����ABC����ACB����180��55����125����
����ABC����ACB����180��55����125����
��2����BDC��90��![]() x����
x����
���ɣ���BD��CD�ֱ�����ABC��ǡ�EBC����FCB��ƽ���ߣ�
���CBD��![]() ����A����ACB������BCD��
����A����ACB������BCD��![]() ����A����ABC����
����A����ABC����
�ߡ�ABC����ACB��180����A��
���BDC��180����CBD��BCD
��180��![]() ����A����ACB����A����ABC��
����A����ACB����A����ABC��
��180��![]() ��2��A��180����A��
��2��A��180����A��
��90��![]() ��A��
��A��
����BDC��90��![]() x����
x����
��3����BDC��![]() ��A��
��A��
���ɣ��������ε�������ʿɵã���ACE����A����ABC����DCE����D����DBC��
��BD��CD�ֱ��ǡ�ABC����ACB��ǡ�ACE��ƽ���ߣ�
���DBC��![]() ��ABC����DCE��
��ABC����DCE��![]() ��ACE��
��ACE��
��![]() ����A����ABC������D��
����A����ABC������D��![]() ��ABC��
��ABC��
���BDC��![]() ��A.
��A.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ж��У���ȷ�ĸ����У� ��
��һ��Ա�ƽ�У�һ��Ա���ȵ��ı�����ƽ���ı��Σ�
�ڶԽ�����ƽ������ȵ��ı����Ǿ��Σ�
�۶Խ����ഹֱ���ı��������Σ�
�ܶԽ����ഹֱƽ������ȵ��ı����������Σ�
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��ax��a��y��![]() ��a��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
��a��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
A.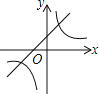 B.
B.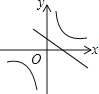
C.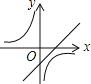 D.
D.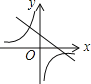
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�п쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ�����������ľ���![]() ��������ʻ��ʱ��
��������ʻ��ʱ��![]() ֮��ĺ�����ϵ��ͼ��ʾ����쳵���ٶ�Ϊ__________��
֮��ĺ�����ϵ��ͼ��ʾ����쳵���ٶ�Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ѵ���ǧ�IJ���ʾ��ͼ����ֹʱ��ǧλ��Ǧ����BD�ϣ�ת��B������ľ���BD=3m��С���ڵ���ǧ�����У�����ǧ�ڶ�����ߵ�Aʱ����õ�A��BD�ľ���AC=2m����A������ľ���AE=1.8m��������A���ڶ���A����ʱ����A'B��AB��
��1����A����BD�ľ��룻
��2����A��������ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ⲻ��ʽ��x+4��3��x��2�����ѽ⼯�������ϱ�ʾ������
![]()
��2��xȡ��Щ����ʱ������ʽ5x��1��3��x+1����![]() ��1�ݩ�2��������
��1�ݩ�2��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AC��BD�ཻ�ڵ�O����E��OA���е㣬����BE���ӳ���AD�ڵ�F����֪S��AEF=4�������н��ۣ���![]() ����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������
����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������
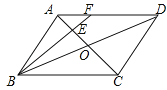
A. �٢ڢۢ� B. �٢� C. �ڢۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣬�ش�����.
���Ƕ�֪��![]() ������������Ϊ������������ѭ��С������˲����ܰ�
������������Ϊ������������ѭ��С������˲����ܰ�![]() ��С������ȫ��д����������С����
��С������ȫ��д����������С����![]() ��ʾ
��ʾ![]() ��С�����֣��������С�ڵ�˼·����������⣺
��С�����֣��������С�ڵ�˼·����������⣺
��1��![]() ���������� ��
���������� ��
��2����֪![]() ����������
����������![]() ��һ������������
��һ������������![]() ��ʾ
��ʾ![]() ��С������.
��������.
��![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
�ڵ�![]() ��5�ı���ʱ����
��5�ı���ʱ����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���ABCD�������Խ��߽��ڵ�O����AB��CD.�����н��ۣ��١�AOB����COD���ƣ��ڡ�ABD����ABC���ƣ���S��COD��S��AOB��DC��AB����S��AOD��S��BOC.������ȷ����(����)
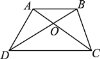
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com