
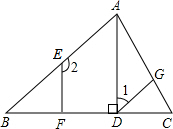
 如图,AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠1+∠2=180°.∠CGD与∠BAC相等吗?为什么?
如图,AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠1+∠2=180°.∠CGD与∠BAC相等吗?为什么?

科目:初中数学 来源: 题型:
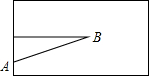 如图所示,立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明的跳远成绩是1.6米,则小明从起跳点到落脚点之间的距离是( )
如图所示,立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明的跳远成绩是1.6米,则小明从起跳点到落脚点之间的距离是( )| A、大于1.6m |
| B、等于1.6m |
| C、小于1.6m |
| D、不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
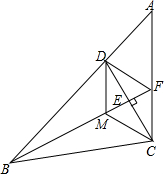 如图,在△ABC中,D是AB上一点,且BD=BC,BF⊥CD于点E,交AC于点F,M为线段BE上任意一点,请探究,当ME与EF满足什么数量关系时四边DMCF是菱形?
如图,在△ABC中,D是AB上一点,且BD=BC,BF⊥CD于点E,交AC于点F,M为线段BE上任意一点,请探究,当ME与EF满足什么数量关系时四边DMCF是菱形?查看答案和解析>>
科目:初中数学 来源: 题型:
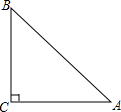 如图,在Rt△ABC中,∠C=90°,∠A=45°.若设BC=x,则AC=
如图,在Rt△ABC中,∠C=90°,∠A=45°.若设BC=x,则AC=查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com