
【题目】如图1,点![]() 、
、![]() ,其中
,其中![]() 、
、![]() 满足
满足![]() ,将点
,将点![]() 、
、![]() 分别向上平移2个单位,再向右平移1个单位至
分别向上平移2个单位,再向右平移1个单位至![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.

(1)直接写出点![]() 的坐标:__________;
的坐标:__________;
(2)连接![]() 交
交![]() 于一点
于一点![]() ,求
,求![]() 的值:
的值:
(3)如图2,点![]() 从
从![]() 点出发,以每秒1个单位的速度向上平移运动,同时点
点出发,以每秒1个单位的速度向上平移运动,同时点![]() 从
从![]() 点出发,以每秒2个单位的速度向左平移运动,设射线
点出发,以每秒2个单位的速度向左平移运动,设射线![]() 交
交![]() 轴于
轴于![]() .问
.问![]() 的值是否为定值?如果是定值,请求出它的值;如果不是定值,请说明理由.
的值是否为定值?如果是定值,请求出它的值;如果不是定值,请说明理由.
【答案】解:(1)![]() ;(2)
;(2)![]() ;(3)证明略;
;(3)证明略;
【解析】
(1)利用非负数的性质,构建方程组即可解决问题.
(2)利用平行线分线段成比例定理即可解决问题.
(3)结论:S△FMD-S△OFN的值是定值.分两种情形:如图2-1中,当点N在线段OB上时,连接OD.如图2-2中,当点N在BO的延长线上时,连接OD.分别说明即可解决问题.
(1)∵![]() ,
,
又∵(3a+b)2≥0,b-a-4≥0,
∴![]() ,
,
解得![]() ,
,
∴A(-1,0),B(3,0),
∴AB=CD=4,
∵OC=2,CD∥AB,
∴D(4,2),
故答案为(4,2).
(2)如图1中,
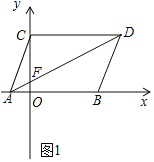
∵CD∥OA,
∴![]() ,
,
∵CD=4,OA=1,
∴![]()
(3)结论:S△FMD-S△OFN的值是定值.
理由:如图2-1中,当点N在线段OB上时,连接OD.
由题意:OM=t,BN=2t,
∴S△OMD=![]() ×t×4=2t,S△DBN=
×t×4=2t,S△DBN=![]() ×2t×2=2t,
×2t×2=2t,
∴S△OMD=S△BND,
∴S四边形DMON=S△OBD=![]() ×3×2=3,
×3×2=3,
∵S△FMD-S△OFN=S四边形DMON=3=定值.
如图2-2中,当点N在BO的延长线上时,连接OD.
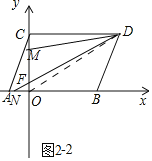
∵S△FMD-S△OFN=S△ODM-S△ODN=S△DBN-S△ODN=S△OBD=3=定值,
综上所述,S△FMD-S△OFN的值是定值,定值为3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在利用正六面体骰子进行频率估计概率的实验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是( )
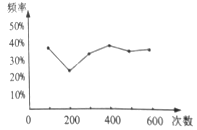
A. 朝上的点数是6的概率B. 朝上的点数是偶数的概率
C. 朝上的点数是小于4的概率D. 朝上的点数是3的倍数的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: A 0,1 , B 2, 0 , C 4, 3 .
(1)求△ABC 的面积;
(2)设点 P 在坐标轴上,且△ABC 和△ABP 的面积相等,直接写出 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体经营户了解到有一种盒装商品能畅销市场,就用4万元购进这种商品,面市后果然供不应求,他又用8.8万元购进了第二批这种商品,所购数量是第一批购进量的2倍,但每盒单价涨了4元,他在销售这种盒装商品时每盒定价都是56元,最后剩下的150盒按八折销售,很快售完,在这两笔生意中,这位个体经营户共赢利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(﹣2,y1),(﹣1,y2),(1,y3)在反比例函数y=![]() 的图象上,则下列说法正确的是( )
的图象上,则下列说法正确的是( )
A.y1>y2>y3 B.y3>y2>y1 C.y3>y1>y2 D.y2>y1>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
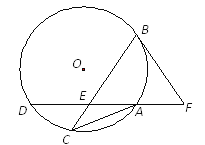
【题目】如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C .
(1)求证:BF是⊙O的切线;
(2)若AD=4,cos∠ABF=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
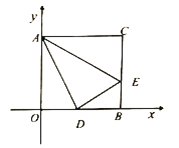
【题目】如图,在平面直角坐标系![]() 中,四边形
中,四边形![]() 为边长为6的正方形,点
为边长为6的正方形,点![]() 为
为![]() 的中点,
的中点,![]() .动点
.动点![]() 在线段
在线段![]() 和
和![]() 上运动,另一动点
上运动,另一动点![]() 在线段
在线段![]() 上运动.
上运动.
用学过的知识解决下列问题:
(1)①填空:点![]() 的坐标____________________;
的坐标____________________;
②求三角形![]() 的面积;
的面积;
(2)求点![]() 在运动过程中,
在运动过程中,![]() 与
与![]() 的数量关系;
的数量关系;
(3)两个动点![]() 在运动过程中,是否存在使线段
在运动过程中,是否存在使线段![]() 的长等于2的时刻,如果存在,求出此时点
的长等于2的时刻,如果存在,求出此时点![]() 坐标;如果不存在,请你说明理由.
坐标;如果不存在,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠A=70°,将平行四边形ABCD绕点B顺时针旋转到平行四边形A1BC1D1的位置,此时C1D1恰好经过点C,则∠ABA1=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校八年级学生每周平均体育锻炼时间的情况,随机抽查了该年级的部分学生,对其每周锻炼时间进行统计,根据统计数据绘制成图1和图2两个不完整的统计图.请你根据统计图提供的信息,回答下列问题:
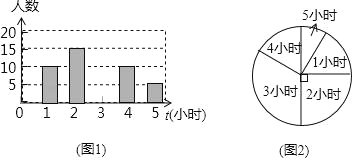
(1)本次共抽取了学生 人,并请将图1条形统计图补充完整;
(2)这组数据的中位数是 ,求出这组数据的平均数;
(3)若八年级有学生1800人,请你估计体育锻炼时间为3小时的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com