
����Ŀ�����Ϲ��涨ÿ���6��5���ǡ����绷���ա���Ϊ��Ͻ���ġ����绷���ա��������ijУ����С���ȫУʦ����չ���ԡ�������������������Ϊ������ʾ��������������������������Ƴ������������ͳ��ͼ��
���У�A���ܽ������ŵ��涨�ĵط������һ��ῼ�������ķ��ࣻ
B���ܽ������ŵ��涨�ĵط��������ῼ�������ķ��ࣻ
C��ż���Ὣ�����ŵ��涨�ĵط���
D����������������
����������Ϣ�ش��������⣺
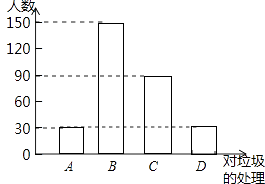
��1����У����С�鹲�����˶����ˣ�����ȫ���������ͳ��ͼ��
��2�������У����ʦ��2400�ˣ���ô��������������Լ�ж����ˣ�
���𰸡�
��1����ͳ��ͼ��֪B���������150�ˣ�ռ��������50%�����Ե����������Ϊ
150��50%=300���ˣ�
D�����������Ϊ300����150+30+90��=30���ˣ�
��ȫͼ��
��2����Ϊ��У����ʦ��2400�ˣ�
��������������������ԼΪ2400�� ![]() =240���ˣ�
=240���ˣ�
����������������Լ��240��
����������1��������ͳ��ͼ֪��B���������150�ˣ�������ͳ��ͼ��֪��B�������ռ��������50%���Ӷ������У����С�鹲���������������ͳ��ͼ�����D���������������2���ɣ�1����֪��D�����������Ϊ300����150+30+90��=30���ˣ����Ӷ����D�������ռ�������İٷֱȣ���֪��У����ʦ��2400�ˣ���������������������������
�����㾫������������ͳ��ͼ������ͳ��ͼ�ǽ����ĸ�������Ҫ֪��������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʿ��ѧ��ŷ����ָ�������Ա�ʾΪ�ĸ�����ƽ��֮�͵ļס���������ˣ���˻���Ȼ���Ա�ʾΪ�ĸ�����ƽ��֮�ͣ��� ![]()
![]() �������������ŷ�����ʽ�����˳���������Ϊ�������ĵ�������ʵ���ϣ��������ۿɸ���Ϊ�����Ա�ʾΪ��������ƽ��֮�͵ļס���������ˣ���˻���Ȼ���Ա�ʾΪ��������ƽ��֮�ͣ�
�������������ŷ�����ʽ�����˳���������Ϊ�������ĵ�������ʵ���ϣ��������ۿɸ���Ϊ�����Ա�ʾΪ��������ƽ��֮�͵ļס���������ˣ���˻���Ȼ���Ա�ʾΪ��������ƽ��֮�ͣ�
���Ķ�˼����
����ѧ˼���У����ֽ��⼼�ɳ�֮Ϊ���������С����������⣺������ʽ ![]() �ij�����ƽ��֮�����ʽ���⣺ԭʽ
�ij�����ƽ��֮�����ʽ���⣺ԭʽ ![]() �q
�q
��1��������һ�ԡ��Խ� ![]() �ij���������ƽ��֮�͵���ʽ�� ��12+52����22+72��=��
�ij���������ƽ��֮�͵���ʽ�� ��12+52����22+72��=��
��2����������⡿�������������������˼��������������ĵ��������⣺������ʽ ![]() �ij���������ƽ��֮�͵���ʽ������a��b��c��d��Ϊ����������������ϸ���Ƶ����̩q
�ij���������ƽ��֮�͵���ʽ������a��b��c��d��Ϊ����������������ϸ���Ƶ����̩q
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b�������и�����ʽ��һ���������ǣ� ��
A.a��1��b��1
B.��a����b
C.![]()
D.ac��bc
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
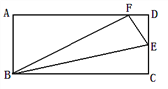
����Ŀ��������9�֣���ͼ����E�Ǿ���ABCD��CD����һ�㣬��BCE��BE�۵�Ϊ��BFE,��F����AD��.
(1)��֤����ABF�ס�DFE
(2)����BEFҲ����ABF���ƣ������![]() ��ֵ .
��ֵ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪б��AB��Ϊ80�ף��½ǣ�����BAC��Ϊ30����BC��AC���ּƻ���б���е�D����ȥ�������壨����Ӱ��ʾ����һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��
��1��������б��BE���½�Ϊ45������ƽ̨DE�ij���������������ţ�
��2��һ��������GH����A��36��Զ����AGΪ36�ף���С����D����ý����ﶥ��H�����ǣ�����HDM��Ϊ30������B��C��A��G��H��ͬһ��ƽ���ڣ���C��A��G��ͬһ��ֱ���ϣ���HG��CG��������GH�ĸ߶ȣ�������������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��չ�ô�μ���������Ϊ20Ԫ������͵���Ϊ80Ԫ������100����
��1���蹺��������Ϊx��������������������ܷ���Ϊy��Ԫ��������д��y��x�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2�����������������ܷ��ò�����6620Ԫ��������������������������3������ô���ļ��ֹ�����
��3���ӽ�Լ��֧�ĽǶ�����������Ϊ�������ַ��������㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com